import numpy as np
import pandas as pd
from scipy import stats

def ttestR(T, df, alpha):   #右侧检验函数
    p=stats.t.sf(T, df)
    return p>=alpha
def ttestL(T, df, alpha):   #左侧检验函数
    p=stats.t.cdf(T, df)
    return p>=alpha

#单样本t检验，检验单个样本数据与某一个数据是否有显著差异。
data = pd.Series([15.6,16.2 ,22.5 ,20.5 ,16.4 ,19.4 ,16.6, 17.9 ,12.7, 13.9])
data_mean = data.mean()
data_std = data.std()
pop_mean=20
#data是样本数据，pop_mean是总体均值 
t,p_towTail = stats.ttest_1samp(data,pop_mean)
print('#单样本t检验')
print(t)
print(p_towTail)

from  scipy.stats import ttest_ind, levene
print('#独立2样本t检验')
# 用于分析定类数据与定量数据之间的关系，如男女生的身高是否有显著差异。
# 独立样本t检验假设样本来自于两个不同的独立总体，但方差相同，
# 除了要求单样本t检验的那些条件，还要求两个样本之间具有方差，需要进行方差齐性检验，参考方差分析。
x = [20.5, 19.8, 19.7, 20.4, 20.1, 20.0, 19.0, 19.9]
y = [20.7, 19.8, 19.5, 20.8, 20.4, 19.6, 20.2]
print(levene(x,y))
print(ttest_ind(x, y))
#levene检验p值大于0.05认为是满足方差齐性的，如果不满足则加一个参数equal_var=False
print(ttest_ind(x,y,equal_var=False))


from  scipy.stats import ttest_rel
# 配对样本t检验
# 配对样本T检验用于分析配对定量数据之间的差异对比关系，这个就和独立样本t检验区分开了，要求样本量相同且前后顺序要一一对应。
# 比如通过两组数据的对比分析，判断背景音乐是否会影响消费行为。配对样本t检验可以通过差值转化为单样本t检验：
x = [20.5, 18.8, 19.8, 20.9, 21.5, 19.5, 21.0, 21.2]
y = [17.7, 20.3, 20.0, 18.8, 19.0, 20.1, 20.0, 19.1]
print('#配对样本t检验')
print(ttest_rel(x, y))



x=np.array([159, 280, 101, 212, 224, 379, 179, 264, #样本数据
           222, 362, 168, 250, 149, 260, 485, 170])
xmean=x.mean()                                      #样本均值
s=x.std(ddof=1)                                     #样本均方差
n=x.size                                            #样本容量
mu0=225                                             #总体均值假设值
alpha=0.05                                          #显著水平
T=(xmean-mu0)/(s/np.sqrt(n))						#检验统计量值
print('#计算左侧检验')
accept=ttestL(T, n-1, alpha)  
print(accept)        				#计算左侧检验
print('mu>=%d is %s.'%(mu0, accept))

T检验是用来比较两个均值之间是否有显著差异的一种检验方法。这一篇给大家介绍一下T检验的种类以及具体的Python实现代码。T检验是比较两个均值差异的，不同种类T检验的差别其实在于均值的计算差异。

1.单样本T检验

单样本T检验是用来检验一组样本的均值A与一个已知的均值B之间是否有差异。均值A是通过一组样本算出来的，均值B是已知的一个具体的值。如下图就是左边样本算出来的均值和值158的对比，此时的t统计量的公式为：

Python实现代码如下：

from scipy import stats
stats.ttest_1samp(data,u)

运行上面的代码会返回t统计量值和对应的p_value。

2.双样本T检验

双样本T检验是用来检验两组样本的均值之间是否有差异。两个均值都是根据样本算出来的。如下图就是左右两部分样本算出来的均值，此时的t统计量的公式为：

Python实现代码如下：

stats.ttest_ind(data1,data2)

3.配对样本T检验

配对样本T检验与双样本T检验有点类似，也是用来检验两组样本的均值差异，只不过普通双样本T检验中的样本是乱序的，而配对样本T检验中的样本是一一对应的。如下图所示，根据经验可得，周一至周五每天的销量不太一样，也不具有可比性，如果是双样本T检验的话就是将周一至周五的销量混在一起，然后对两组销量进行对比，但是这样显然是不太合理，正确的应该是周一和周一比，周二和周二比，总而言之，就是具有相同属性的数据之间进行相比，而不是混合总体进行相比。此时的t统计量公式为：

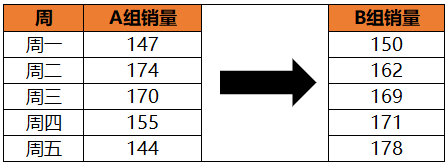
Python实现代码如下：

stats.ttest_rel(data1,data2)