Baum-Welch算法

Baum-Welch算法可以解决无监督学习的隐马尔可夫问题，也即是说，如果如果我们现在有一个训练集没有状态序列，只有观测序列，现在让我们根据观测序列求隐马尔可夫模型参数及：Z=(A,B,C).那么就可以用Baum-Welch算法来解决该问题。将状态序列看做隐变量I.那么我们要学习的模型可以表示为下式：

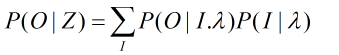
在这里插入图片描述
提到隐变量，如果你看过我之前的博客应该知道怎么求解上面这个问题了吧，可以用EM算法求解上述最优解的问题。这里就不多说了，直接套公式最后求导就可以解决。

Logo
加入社区！打开量化的大门，首批课程上线啦！

加入社区！打开量化的大门，首批课程上线啦！

更多推荐

cover

python爬虫入门案例day05:Pexels

avatar 量化交易与投资社区

终极指南：如何避免RateLimitExceededException的Laravel API安全防护

在构建RESTful API时，避免RateLimitExceededException是每个开发者必须掌握的关键技能。Dingo API作为Laravel和Lumen框架的强大RESTful API包，提供了完整的速率限制机制来保护你的应用程序免受恶意请求和过量访问。本文将为你详细介绍如何配置和使用这些安全功能。## 🛡️ 什么是速率限制及其重要性速率限制是API安全的第一道防线，它能

avatar 量化交易与投资社区

xxHash算法的学术研究：引用分析与相关改进论文综述

xxHash作为当前最快的非加密哈希算法，在学术界和工业界都引起了广泛关注。其极致的速度和优秀的质量特性使其成为哈希算法研究的重要对象。本文将深入分析xxHash在学术研究中的引用情况，并综述相关的改进论文和研究进展。## 📊 xxHash算法概述与技术特点xxHash是由Yann Collet开发的一种极速非加密哈希算法，主要包含三个版本：XXH32（32位哈希）、XXH64（64位哈

avatar 量化交易与投资社区