1.递归实现指数型枚举

https://www.acwing.com/problem/content/94/

枚举每个位置选还是不选

#include<iostream>
using namespace std;
const int N = 20;
int vis[N];
int n;

//u是当前枚举的位置，一共要枚举n位，分别枚举每位选还是不选
void dfs(int u){
    if(u > n){
        for(int i = 1; i <= n; i++){
            //如果选了就输出
            if(vis[i]){
                cout<<i<<" ";
            }
        }
        cout<<endl;
        return;
    }
    //不选
    vis[u] = 0;
    dfs(u + 1);
    
    //选
    vis[u] = 1;
    dfs(u + 1);
}

int main(){
    cin>>n;
    dfs(1);
    return 0;
}

2.递归实现组合型枚举

https://www.acwing.com/problem/content/95/

每次枚举m个数，标记每次开始枚举的位置

#include<iostream>
using namespace std;
const int N = 30;
int a[N];
int n, m;

//u是枚举的第几位，st是从哪一位开始枚举
void dfs(int u, int st){
    if(u > m){
        for(int i = 1; i <= m; i++){
            cout<<a[i]<<" ";
        }
        cout<<endl;
        return;
    }
    //从st开始枚举
    for(int i = st; i <= n; i++){
        a[u] = i;
        dfs(u + 1, i + 1);
    }
}

int main(){
    cin>>n>>m;
    dfs(1, 1);
    return 0;
}

3.递归实现排列型枚举

https://www.acwing.com/problem/content/96/

每次标记用过的数，递归完一轮后再恢复现场

#include<iostream>
using namespace std;
const int N = 10;
int vis[N], a[N];
int n;

//u是当前枚举的位置
void dfs(int u){
    if(u > n){
        for(int i = 1; i <= n; i++){
            cout<<a[i]<<" ";    
        }
        cout<<endl;
        return;
    }
    for(int i = 1; i <= n; i++){
        if(!vis[i]){
            //标记用过的元素
            vis[i] = 1;
            a[u] = i;
            dfs(u + 1);
            //恢复现场
            vis[i] = 0;
        }
    }
}

int main(){
    cin>>n;
    dfs(1);
    return 0;
}

//或者用库函数
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 10;
int a[N];
int n;

int main(){
    cin>>n;
    //第一个排列
    for(int i = 1; i <= n; i++){
        a[i] = i;
    }
    do{
        for(int i = 1; i <= n; i++){
            cout<<a[i]<<" ";
        }
        cout<<endl;
    }while(next_permutation(a + 1, a + n + 1));
    return 0;
}

4.费解的开关

https://www.acwing.com/problem/content/97/

枚举每一种情况

#include<iostream>
using namespace std;
const int N = 5;
char g[N][N];

void t(int x, int y){
    int dx[] = {0, -1, 0, 1, 0};
    int dy[] = {-1, 0, 1, 0, 0};
    //改变五个位置灯的状态
    for(int i = 0; i < 5; i++){
        int a = x + dx[i], b = y + dy[i];
        if(a >= 0 && a < 5 && b >= 0 && b < 5){
            //相同为0，不同为1，字符也可以用
            g[a][b] ^= 1;
        }
    }
}

void f(){
    int ans = INT32_MAX;
    //二进制下为1的位置，就改变这个位置的状态
    for(int k = 0; k < (1 << 5); k++){
        int cnt = 0;
        //临时存储
        char b[N][N];
        //或者用memcpy(b, g, sizeof(g));
        for(int i = 0; i < 5; i++){
            for(int j = 0; j < 5; j++){
                b[i][j] = g[i][j];
            }
        }
        //改变第一行
        for(int j = 0; j < 5; j++){
            if(k >> j & 1){
                t(0, j);
                cnt++;
            }
        }
        //根据第一行状态的变化，改变剩下三行
        for(int i = 1; i < 5; i++){
            for(int j = 0; j < 5; j++){
                if(g[i - 1][j] == '0'){
                    t(i, j);
                    cnt++;
                }
            }
        }
        int flag = 1;
        //判断最后一行是否全亮
        for(int j = 0; j < 5; j++){
            if(g[4][j] == '0'){
                flag = 0;
                break;
            }
        }
        //求所有方案的最小操作数
        if(flag){
            ans = min(ans, cnt);
        }
        for(int i = 0; i < 5; i++){
            for(int j = 0; j < 5; j++){
                g[i][j] = b[i][j];
            }
        }
    }
    if(ans <= 6){
        cout<<ans<<endl;
    }else{
        cout<<-1<<endl;
    }
}

int main(){
    int n;
    cin>>n;
    while(n--){
        for(int i = 0; i < 5; i++){
            for(int j = 0; j < 5; j++){
                cin>>g[i][j];
            }
        }
        f();
    }
    return 0;
}

5.奇怪的汉诺塔

三个柱子：d[n] = 2 * d[n - 1] + 1;
把前面 n - 1 个盘子从 A 移到 B，然后把剩下一个盘子移到 C，然后把 B 柱子上的盘子移到 C

四个柱子：f[n] = min{2 * f[i] + d[n - i]}
初始化：f[1] = 1(一个盘子在4塔模式下移动到D柱需要1步)
先把i个盘子在4塔模式下移动到B柱，
然后把n-i个盘子在3塔模式下移动到D柱（因为不能覆盖到B柱上，就等于只剩下A、C、D柱可以用）
最后把i个盘子在4塔模式下移动到D柱
考虑所有可能的i取最小值，即得到上述递推公式

#include<iostream>
#include<cstring>
using namespace std;
const int N = 20;
int d[N], f[N];
int n;

int main(){
    n = 12;
    for(int i = 1; i <= n; i++){
        d[i] = 2 * d[i - 1] + 1;
    }
    memset(f, 0x3f, sizeof(f));
    f[1] = 1;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j < i; j++){
            f[i] = min(f[i], 2 * f[j] + d[i - j]);
        }
    }
    for(int i = 1; i <= n; i++){
        cout<<f[i]<<endl;
    }
    return 0;
}

6.约数之和

https://www.acwing.com/problem/content/99/

#include<iostream>
#include<unordered_map>
using namespace std;
const int mod = 9901;
//存储质因子和出现的次数
unordered_map<int, int> primes;

//试除法分解质因子
void divide(int n){
    for(int i = 2; i <= n / i; i++){
        if(n % i == 0){
            while(n % i == 0){
                primes[i]++;
                n /= i;
            }
        }
    }
    if(n > 1){
        primes[n]++;
    }
}

//计算a^b
int qmid(int a, int b){
    int res = 1;
    while(b){
        if(b & 1) res = (long long)res * a % mod;
        a = (long long)a * a % mod;
        b >>= 1;
    }
    return res;
}

//计算p^0 + ... + p^k
int sum(int p, int k){
    if(k == 1) return 1;
    if(k % 2 == 0){
        return (long long)(qmid(p, k / 2) + 1) * sum(p, k / 2) % mod;
    }else{
        //奇数的时候，转化为偶数情况
        return (qmid(p, k - 1) + sum(p, k - 1)) % mod;
    }
}

int main(){
    int A, B;
    cin>>A>>B;
    //对A分解质因数
    divide(A);
    //存储答案
    int res = 1;
    for(auto it : primes){
        int p = it.first, k = it.second * B;
        //有k个出现次数，还有为0的情况，加起来为k+1
        res = (long long)res * sum(p, k + 1) % mod;
    }
    if(!A) res = 0;
    cout<<res;
    return 0;
}

7.分形之城

https://www.acwing.com/problem/content/100/

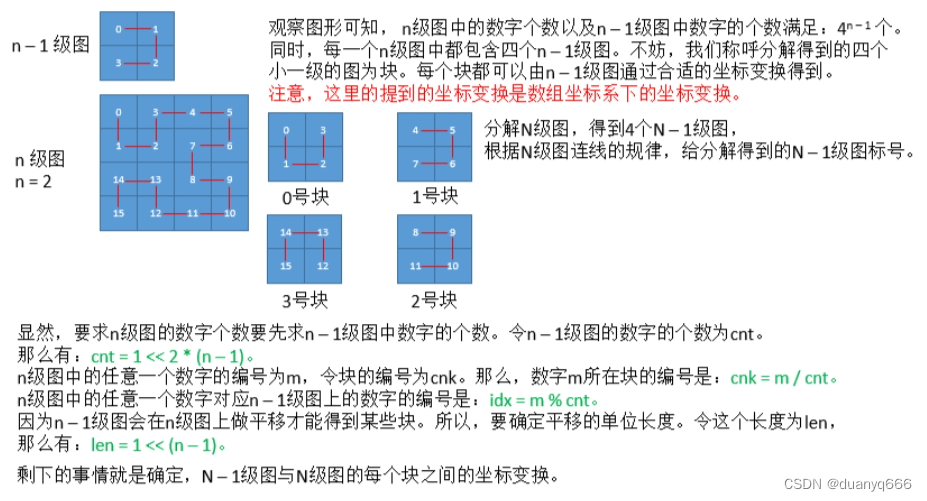
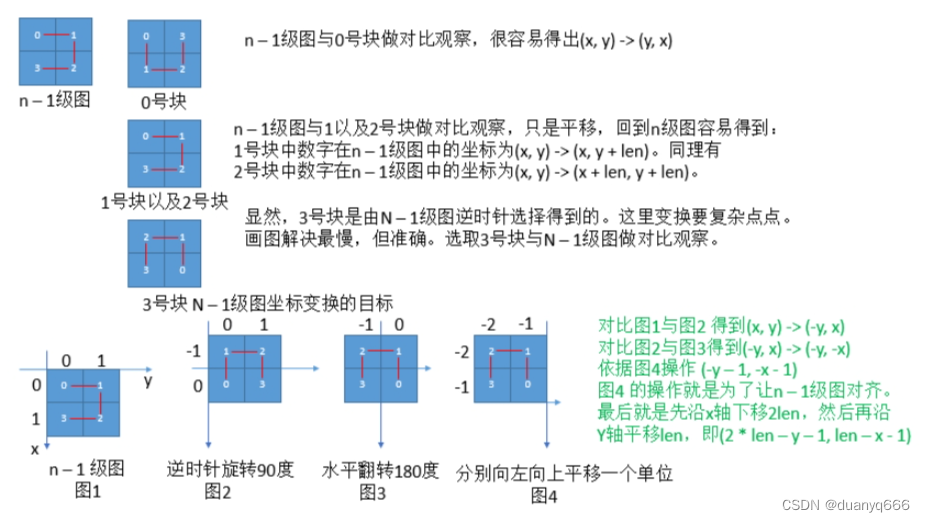
#include<iostream>
#include<cmath>
using namespace std;

pair<long, long> calc(long long n, long long m){
    if(n == 0) return {0, 0}; //或make_pair(0, 0)
    long long len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
    auto pos = calc(n - 1, m % cnt); //n级图中，m元素所属块中的坐标
    long long x = pos.first, y = pos.second;
    long long z = m / cnt; //n级图中，m元素所属块的编号
    if(z == 0) return {y, x}; 
    if(z == 1) return {x, y + len}; 
    if(z == 2) return {x + len, y + len}; 
    if(z == 3) return {2 * len - y - 1, len - x - 1}; 
}

int main(){
    int t;
    cin>>t;
    while(t--){
        long long n, a, b;
        cin>>n>>a>>b;
        auto ac = calc(n, a - 1); 
        auto bc = calc(n, b - 1); 
        double x = ac.first - bc.first, y = ac.second - bc.second;
        long long res = round(sqrt(x * x + y * y) * 10); //四舍五入
        cout<<res<<endl;
    }
    return 0;
}