一 经典马科维茨投资组合（classical Markowitz model）

1952年哈里马科维茨发表了一篇题为“证劵组合选择”的论文，标志着现代证劵组合理论的开端。在单期投资中，投资者分别以预定资金比例购买并持有的一个证劵组合（Portfolio）到期末，马科维茨模型试图通过优化Portfolio来获取风险和收益的最佳点。

马科维茨投资组合的三个假设前提：

1. 单一投资期；
2. 流动性很高，无交易成本；
3. 投资者的选择基于最优均值方差；

考虑一个Portfolio，其中：
每种资产的权重为$w_1$,$w_2$,…$w_n$，资产组合权重向量记为$w$，
每种资产收益的随机变量为$R_1$,$R_2$,…$R_n$，
每种资产的平均收益率(也即收益率期望)为${\mu }_1$,${\mu }_2$,…${\mu }_n$，其中${\mu }_i=E(R_i)$，资产收益率期望向量记为$\mu$，
资产i的收益跟资产j的收益的协方差为 ${\sigma }_{i,j}=COV(R_i,R_j)=E(R_i{R}_j)-E(R_i)E(R_j)$，
收益相关性矩阵$C$为两两资产收益的协方差矩阵，
$C=\left[\begin{array}{cccc}var(x_1)& cov(x_1,x_2)& ...& cov(x_1,x_n)\\ cov(x_2,x_1)& var(x_2)& ...& cov(x_2,x_n)\\ ...& ...& ...& ...\\ cov(x_n,x_1)& cov(x_n,x_2)& ...& var(x_n)\end{array}\right]$
整个Portfolio的收益率期望$E(R_P)=\sum _{i=1}^n{w}_{i}E(R_i)={\mu }^{T}w$，
整个Portfolio的风险（也即波动性）可以使用收益的方差来衡量，收益的方差为: $w^{T}Cw$,

1.1 优化问题A

在限定收益的前提下，最小化风险，数学表达为：
min $w^{T}Cw$
s.t.

1. $\Sigma w_i=1$ (该限制条件理解为：权重和为1 )
2. ${\mu }^{T}w>=\rho$ (该限制条件理解为：确保总收益最小为$\rho$)
3. $w_1,w_2,...w_n>=0$ （该限制条件理解为每个权重大于0，也即不允许卖空。实际上最基本的问题并不包含最后这一个不等式条件。但这是一个常见条件，我们把它写在这里。）

1.2 优化问题B

在控制风险的前提下，最大化收益，数学表达为：
max ${\mu }^{T}w$
s.t.

1. $\Sigma w_i=1$
2. $w^{T}Cw>=\beta$
3. $w_1,w_2,...w_n>=0$

1.3 优化问题C

多目标问题，在风险和收益的比例参数化后，最小化它们的混合，数学表达为：
min $-\lambda {\mu }^{T}w+w^{T}Cw$
s.t.

1. $\Sigma w_i=1$
2. $w_1,w_2,...w_n>=0$

上述三种优化问题中，每一种都有一个参数 $\rho$, $\beta$, $\lambda$，其值决定了风险和收益的取舍。从直观也能感受到，三者具有某种等价性。在阐释其等价性之前，我们需要先了解什么是有效前沿。

有效前沿 Efficient Frontier

回到优化问题A，我们将固定的总收益$\rho$进行增加或减小会得到什么样的结果呢？我们将总平均收益和方差的关系画成曲线，是一个横向的二次函数（这里用函数不是很恰当，因为是横向的）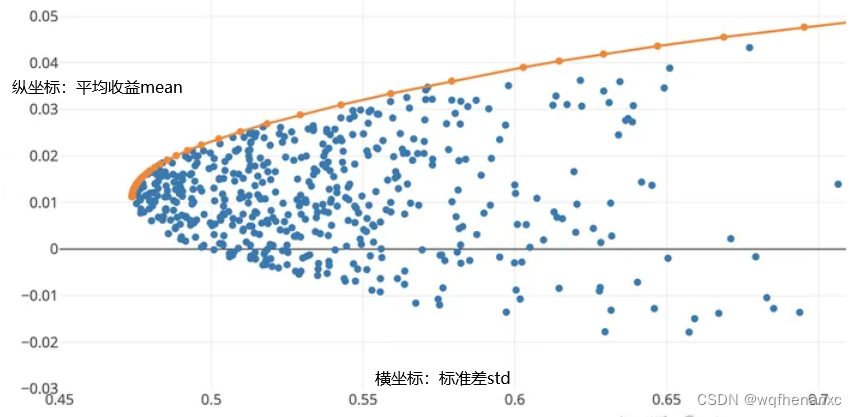

图中，纵坐标为平均收益mean，横坐标为标准差std(和方差是差不多，图会瘦一点）, 蓝色的点为可行域。桔色的线布满了可行域的上半边，桔色线上的每个点对应固定平均收益下的最优风险点，称为有效前沿 — efficient frontier。在有效前沿上从一点抵达另一点必须对风险和收益进行取舍(trade off), 这些点也称作是 non-dominated 的（不只是存在唯一的最优解，而是一组具有同等优化级别的无支配（Non-Dominated）解 ）。

此外请注意这个图描述的是允许卖空的情况。对于有权重大于0的约束，可行域要小很多，但有效前沿依然存在。

【1】https://zhuanlan.zhihu.com/p/353421604 知乎：深入理解马科维茨投资组合
【2】https://zhuanlan.zhihu.com/p/37446641 知乎：从均值方差到有效前沿