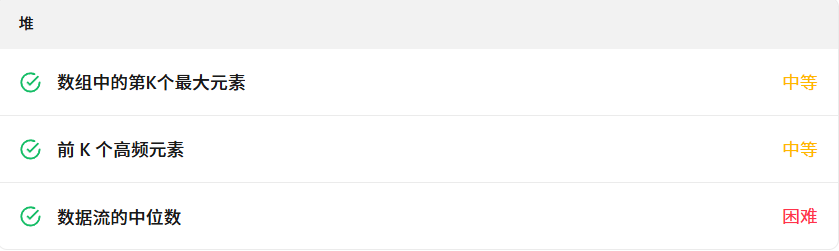
这个专题我们要知道,需要掌握什么基础知识开刷?看见什么题的时候想到这个数据结构呢?

我们要从与他相近的栈来对比.
栈维护的数据顺序,堆维护元素频率

也就是说堆通过使用大顶堆,小顶堆,来维持了元素的排序

栈的话保存的是放入放出的顺序.

高频的基础api

PriorityQueue（优先级队列）是基于堆实现的，默认是小顶堆（最小的元素在队首）。它在处理Top K和中位数这类问题上非常高效

堆的常用操作如下：

------------------逐题思路+代码-----------------------------

思路:

1.直接sort排序然后n-k就是(可以回家等通知了)

2.用堆排序(下一次二刷实现我会补上)

3.分组快排(我使用到的)

思想是通过一个随机数为基准,划分 大,等于,小,这三个集合

每一次循环判断当前k在这三个组哪个里面,如果在等于里面,那就可以返回答案了,如果在大于里面,还需要进一步缩小范围

如果在小于基准组里面,调整k继续递归.

如果想节省空间开销可以直接用原来数组操作,我这里学到的第一版是集合返回值,我就直接套进来了

代码:

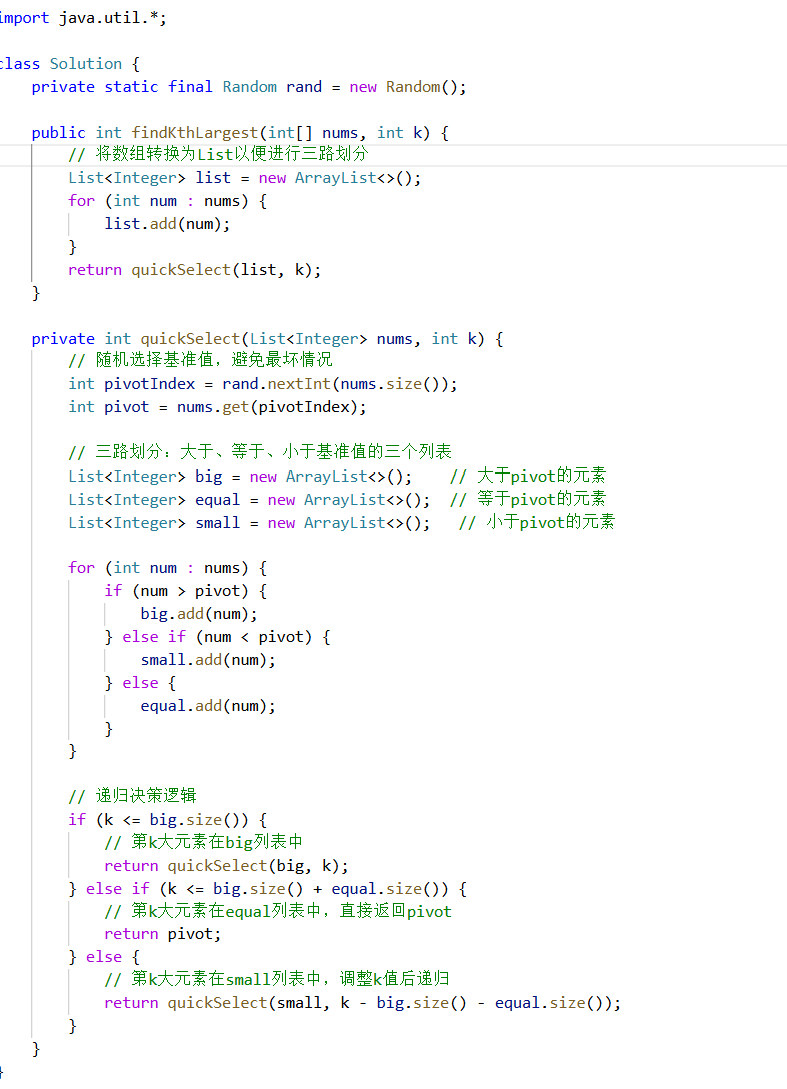
import java.util.*;

class Solution {
    private static final Random rand = new Random();
    
    public int findKthLargest(int[] nums, int k) {
        // 将数组转换为List以便进行三路划分
        List<Integer> list = new ArrayList<>();
        for (int num : nums) {
            list.add(num);
        }
        return quickSelect(list, k);
    }
    
    private int quickSelect(List<Integer> nums, int k) {
        // 随机选择基准值，避免最坏情况
        int pivotIndex = rand.nextInt(nums.size());
        int pivot = nums.get(pivotIndex);
        
        // 三路划分：大于、等于、小于基准值的三个列表
        List<Integer> big = new ArrayList<>();    // 大于pivot的元素
        List<Integer> equal = new ArrayList<>();  // 等于pivot的元素  
        List<Integer> small = new ArrayList<>();   // 小于pivot的元素
        
        for (int num : nums) {
            if (num > pivot) {
                big.add(num);
            } else if (num < pivot) {
                small.add(num);
            } else {
                equal.add(num);
            }
        }
        
        // 递归决策逻辑
        if (k <= big.size()) {
            // 第k大元素在big列表中
            return quickSelect(big, k);
        } else if (k <= big.size() + equal.size()) {
            // 第k大元素在equal列表中，直接返回pivot
            return pivot;
        } else {
            // 第k大元素在small列表中，调整k值后递归
            return quickSelect(small, k - big.size() - equal.size());
        }
    }
}

----------------------------------------------------------------------------------------

其实这也就是堆与栈的区别,栈维护的数据顺序,堆维护元素频率

思路:

先给数组排序

经过遍历排序,把一个一个的哈希映射对应上map

然后用最小堆(k)来维护元素,

最后返回
 

这道题有好多集合的api我忘记了

Map.containsKey    (忘记加s)

For(类型 元素:集合)  (增强for)

Map.keySet 获得所有key放set集合里

Pq.remove移出最上面 ,pq.poll也是移出上面

Pq.peek看最上面的

优先队列的创建与修改存放顺序

这样小的在上面大的在下面(按频率,存放的是元素)

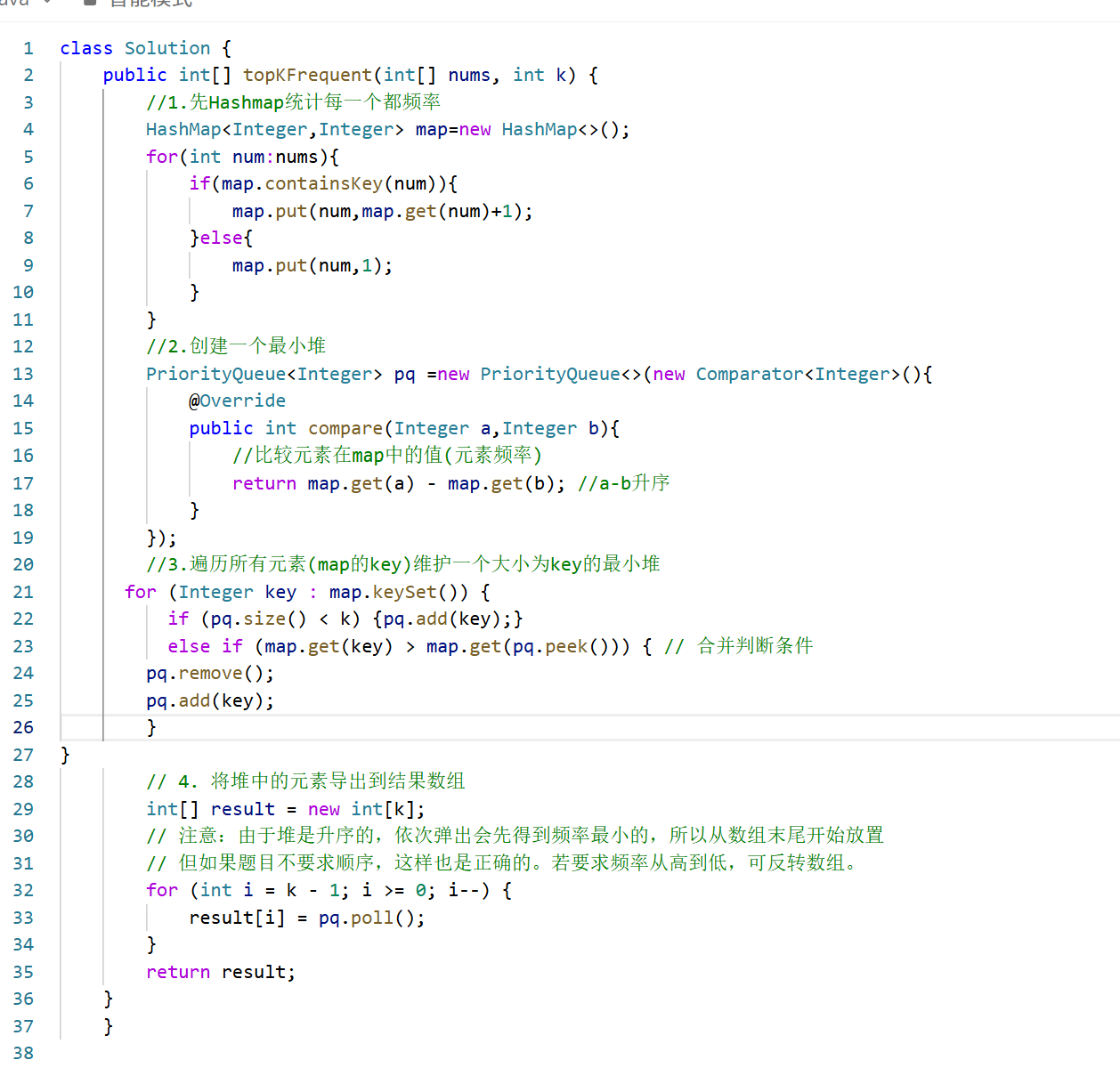
代码:

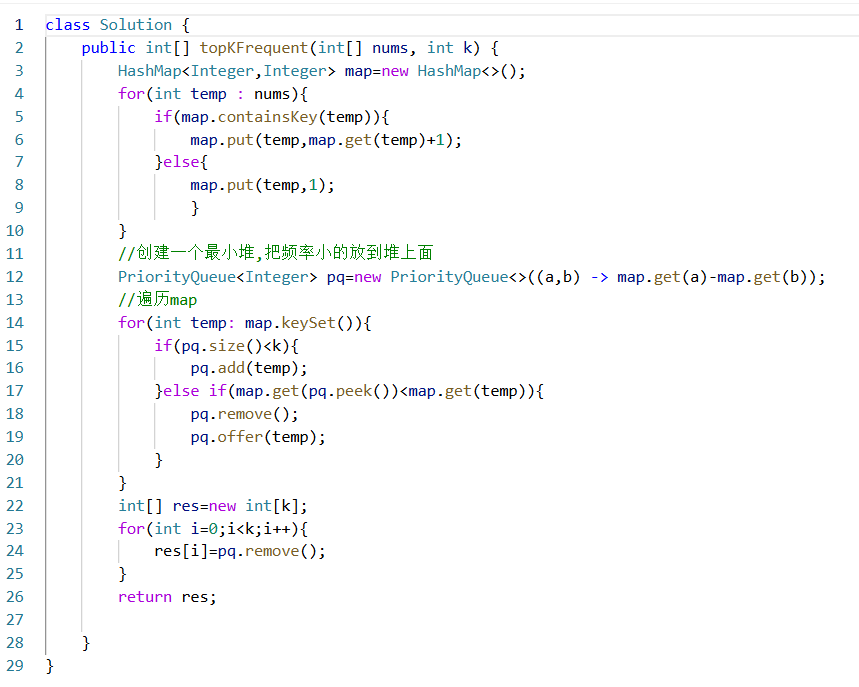
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        HashMap<Integer,Integer> map=new HashMap<>();
        for(int temp : nums){
            if(map.containsKey(temp)){
                map.put(temp,map.get(temp)+1);
            }else{
                map.put(temp,1);
                }
        }
        //创建一个最小堆,把频率小的放到堆上面
        PriorityQueue<Integer> pq=new PriorityQueue<>((a,b) -> map.get(a)-map.get(b));
        //遍历map
        for(int temp: map.keySet()){
            if(pq.size()<k){
                pq.add(temp);
            }else if(map.get(pq.peek())<map.get(temp)){
                pq.remove();
                pq.offer(temp);
            }
        }
        int[] res=new int[k];
        for(int i=0;i<k;i++){
            res[i]=pq.remove();
        }
        return res;

    }
}

----------------------------------------------------------------------------------------

思路:老实说我题没看懂,但是看过

Krahets大佬的评论图片恍然大悟,链接我放下面

https://leetcode.cn/problems/find-median-from-data-stream/solutions/2361972/295-shu-ju-liu-de-zhong-wei-shu-dui-qing-gmdo

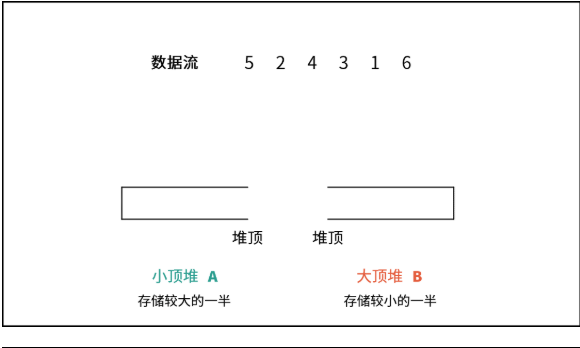
主要是维护这样的两个堆,一个小顶堆,一个大顶堆,依次来存放数据和查询中位数,大小各左右分配,中位数就是两个堆顶,上的数据,保证A的始终优先多一个,奇数就先拿A.peek.否则就A.peek和B.peek去计算一下和.

怎么维护一大一下呢,就是要在添加的时候操作,一次一边新加数据就把弹出的数据加到另一边.每次加的时候默认排序.

代码:

class MedianFinder {
   PriorityQueue<Integer> A,B;
    public MedianFinder() {
        A=new PriorityQueue<>(); //小顶堆,保留大的一半,因为大的放在底下
        B=new PriorityQueue<>((a,b)->(b-a));//大顶堆,保存较小的一半,因为小的在底下
    }
    
    public void addNum(int num) {
        if(A.size() != B.size()){
            //加上新来的,正好是奇数,加的a里面自动排序,然后把a里面最小的弹出放到b
            A.add(num);
            B.add(A.poll());
        }else{
            //与上面相反
            B.add(num);
            A.add(B.poll());
        }
        
    }
    
    public double findMedian() {
        return A.size()!=B.size() ? A.peek() :(A.peek() + B.peek()) / 2.0;
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */