通信系统中概率整形技术(Probability Shaping, PS)详解
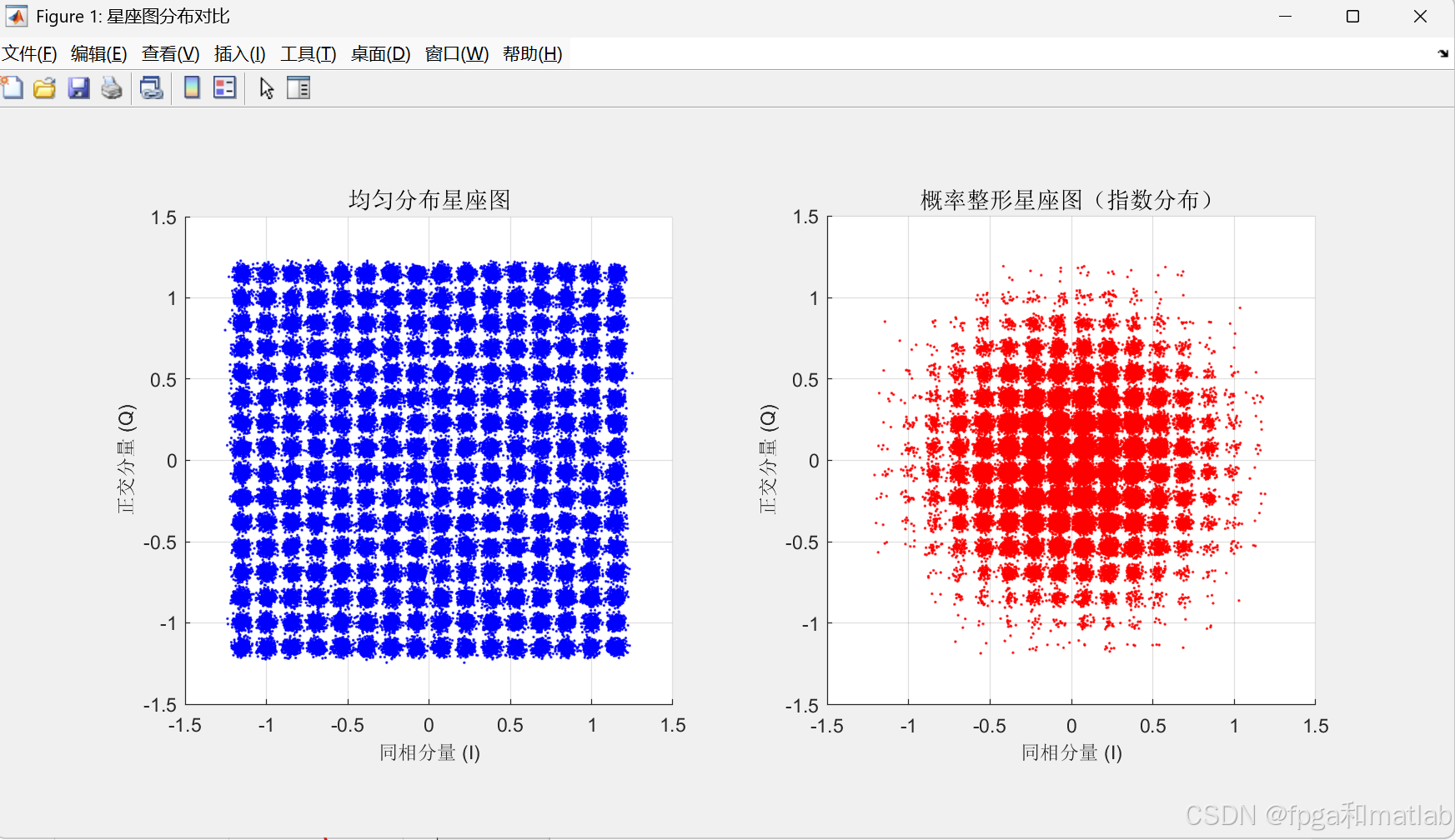
概率整形技术通过优化信号星座点分布提升通信性能。该技术利用非均匀概率分布(低能量星座点出现更频繁),相比传统均匀分布可提高频谱效率或降低发射功率。文章详细介绍了概率整形原理、星座图定义及MATLAB仿真实现,通过对比16QAM调制下均匀分布与指数分布的性能差异,验证了概率整形在逼近香农极限方面的优势。仿真结果显示,概率整形星座图中低能量点分布更密集,适用于5G/6G光通信等功率受限场景。
目录
概率整形是数字通信中一种通过优化信号星座点概率分布来提升传输性能的技术。传统数字调制(如QAM、PSK)采用均匀概率分布(每个星座点出现概率相同),但这种方式未充分利用信道容量 —— 在相同平均功率下,非均匀分布(低能量星座点出现概率更高)可携带更多信息,或在相同速率下降低平均发送功率。
概率整形的核心优势在于:
逼近香农极限:通过匹配信道容量的概率分布(如高斯分布),提升频谱效率;
功率效率优化:降低平均发送功率,尤其适用于功率受限场景(如光纤通信、卫星通信);
兼容性强:可与现有调制(如16QAM、64QAM)及编码(如LDPC、Polar码)结合使用。
目前,概率整形已成为高速光通信(如5G/6G承载网、数据中心互联)的关键技术之一。
1.概率整形的基本原理
概率整形的核心是通过分布匹配(Distribution Matching)技术,将均匀分布的二进制信息序列转换为符合目标概率分布的星座点索引序列,使发送的星座点概率非均匀化(低能量点概率更高),最终在接收端通过分布解匹配恢复原始信息。
具体流程如下:
1.信息源:生成均匀分布的二进制比特流(0和1出现概率均为0.5);
2.分布匹配:将输入比特流映射为星座点索引序列,使索引对应的星座点概率符合预设的非均匀分布(如高斯近似分布);
3.调制:根据索引选择星座点,进行传统调制(如QAM);
4.信道传输:信号经过AWGN、衰落等信道;
5.解调与检测:接收端解调并通过最大似然(ML)或软解调获取星座点索引估计;
6.分布解匹配:将索引估计转换为二进制比特流,恢复原始信息。
2.星座与概率分布定义


3.MATLAB仿真程序
% 概率整形技术仿真:带星座图分布的16QAM性能对比
clear; clc; close all;
%% 1. 参数设置
M = 256; % 256QAM星座点数
k = log2(M); % 每个符号的比特数(均匀分布时)
EbN0_dB = 0:2:26; % 信噪比范围(dB)
EbN0 = 10.^(EbN0_dB/10); % 转换为线性值
N_sym = 1e6; % 每个信噪比下的符号数
% 生成16QAM星座(归一化平均功率为1)
constellation = qammod(0:M-1, M, 'UnitAveragePower', true);
E = abs(constellation).^2; % 各星座点能量
%% 2. 定义目标概率分布(非均匀分布:指数分布)
lambda = 0.9999998; % 指数分布参数(控制分布形状)
p_nonuniform = exp(-lambda * E*5); % 指数分布概率
p_nonuniform = p_nonuniform / sum(p_nonuniform); % 归一化
p_uniform = ones(1, M) / M; % 均匀分布概率
%% 3. 分布匹配器(基于累积分布函数的映射)
function indices = distribution_matcher(p, N)
cdf = cumsum(p); % 累积分布函数
r = rand(1, N); % 均匀随机数
% 将随机数映射到星座点索引
indices = arrayfun(@(x) find(cdf >= x, 1), r);
end
%% 4. 生成星座图数据并显示
% 生成足够多的符号以展示分布特性
N_plot = 1e5;
% 生成均匀分布星座点
indices_uniform = randi([1, M], 1, N_plot);
symbols_uniform = constellation(indices_uniform);
% 生成概率整形星座点
indices_nonuniform = distribution_matcher(p_nonuniform, N_plot);
symbols_nonuniform = constellation(indices_nonuniform);
symbols_uniform2 = symbols_uniform + 0.025 * (randn(1, length(symbols_uniform)) + 1i*randn(1, length(symbols_uniform)));
symbols_nonuniform2= symbols_nonuniform + 0.025 * (randn(1, length(symbols_nonuniform)) + 1i*randn(1, length(symbols_nonuniform)));
% 绘制星座图分布
figure('Name', '星座图分布对比', 'Position', [100, 100, 1000, 500]);
% 均匀分布星座图
subplot(1, 2, 1);
scatter(real(symbols_uniform2), imag(symbols_uniform2), 10, 'b', '.');
title('均匀分布星座图', 'FontSize', 12);
xlabel('同相分量 (I)', 'FontSize', 10);
ylabel('正交分量 (Q)', 'FontSize', 10);
axis equal;
grid on;
xlim([-1.5 1.5]);
ylim([-1.5 1.5]);
% 概率整形星座图
subplot(1, 2, 2);
scatter(real(symbols_nonuniform2), imag(symbols_nonuniform2), 10, 'r', '.');
title('概率整形星座图(指数分布)', 'FontSize', 12);
xlabel('同相分量 (I)', 'FontSize', 10);
ylabel('正交分量 (Q)', 'FontSize', 10);
axis equal;
grid on;
xlim([-1.5 1.5]);
ylim([-1.5 1.5]);
测试结果如下:
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)