目录

 

一、题

二、暴力法分析（为什么会超时）

三、莫队算法

1. 什么是莫队算法？

(1) 使用条件

(2) 核心思想

（3）分块策略

2. 题目如何套用莫队

四、详细步骤

步骤 1：定义结构体保存查询

步骤 2：对查询排序

步骤 3：维护两个辅助数组

步骤 4：add() 和 del() 操作

步骤 5：双指针执行所有查询

五、完整代码

六、莫队算法知识点总结

七、总结

---

 

一、题目

9.重复的数 - 蓝桥云课

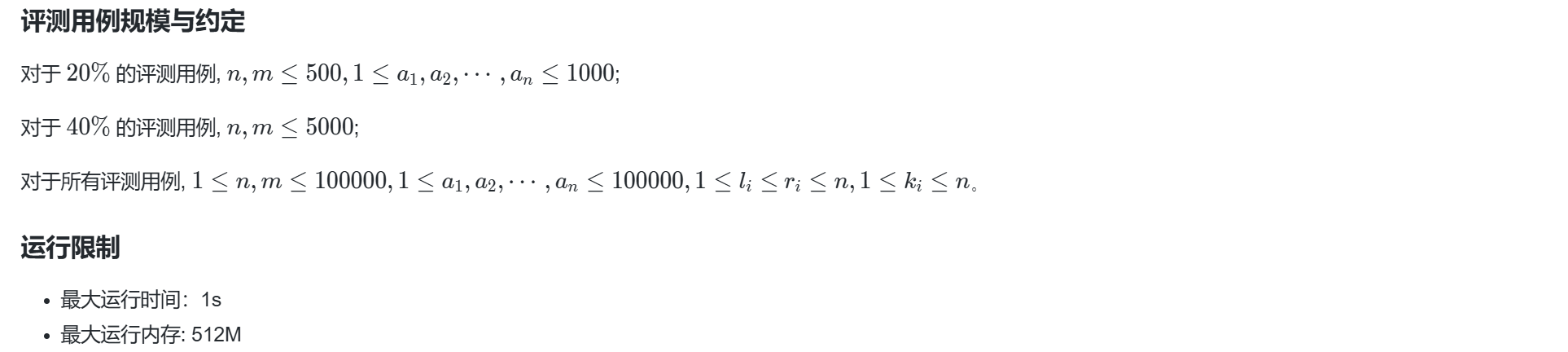
【将题目抽象过来即】：

给定一个长度为 n 的整数序列 A，以及 m 个查询。每个查询包含三个数 (l, r, k)，求：

数组 A 的第 l 到第 r 个数中，恰好出现 k 次的不同整数有多少个？

 

二、暴力法分析（为什么会超时）

最直接的做法是，对每个 (l, r, k) 查询：

• 遍历子数组 A[l..r]

• 用哈希表记录每个数字出现了多少次

• 最后统计出现次数为 k 的数有几个

时间复杂度是 O(n * m)，也就是最多需要一万亿次操作（当 n=m=1e5 时），会超时

 

三、莫队算法

我们可以使用莫队算法优化查询，使得总时间降为大约 O(n*√n)

1. 什么是莫队算法？

莫队是一种适用于离线区间查询的问题的算法

❗适用于查询区间，但不支持修改操作

(1) 使用条件

• 数组是固定的（不修改）

• 所有查询可以提前读入（离线处理）

• 查询是关于某个区间 [l, r] 的

(2) 核心思想

1.将所有查询提前读入（结构体保存）

莫队算法通常需要维护一个查询结构体，将我们要查询的信息放进去

（取决于题目的具体问题）

比如：

- 查询区间的左右端点

- 在查询区间内我们需要维护/求的值

......

2. 将查询排序，按照块编号+右端点排序（块号小的优先，如果块号相同，右端点小的优先），减少移动次数

3.用两个指针 l 和 r 维护当前区间

4.通过 add（）【扩展区间】和 del()【缩小区间】操作增量更新统计值

5.每次查询直接读出答案

（3）分块策略

设定块大小为 sqrt(n)，把整个查询按照：

• 左端点所在的块编号升序排序

• 块内再按照右端点升序排序

这样可以控制指针左右滑动次数在最少范围

 

2. 题目如何套用莫队

我们的问题是：

统计某区间内出现次数恰好为 k 的不同数有多少个？

所以我们需要：

• cnt[x]：记录某个数 x 在当前区间中出现的次数

• sum[times]：表示当前区间内有多少个数，它们的出现次数正好是times

这样我们每次查询，只需读取 sum[k] 即可

 

四、详细步骤

步骤 1：定义结构体保存查询

struct Node
{
  int id;//原始序列号，方便输出的时候按照顺序
  int l,r,k;//区间边界值，出现k的次数
}node[N]

我们需要保留 id 来在排序后还原原始顺序

---

步骤 2：对查询排序

使用块排序策略：

//查询结构体排序
bool cmp(const Node& a,const Node& b)
{
  //属于同一块，右端点小的优先
  if(a.l/len==b.l/len) return a.r<b.r;
  //否则，块小的优先
  else return a.l/len<b.l/len;
}

len=sqrt(n) 是经验最优分块大小

---

步骤 3：维护两个辅助数组

int sum[N];//恰好出现i次的数的个数
int cnt[N];//i在区间内出现的次数

---

步骤 4：add() 和 del() 操作

用于在区间中加入或移除某个数（通过移动指针实现）：

//扩展区间
void add(int i)
{
  sum[cnt[i]]--;//出现次数为cnt[i]的数的个数-1
  cnt[i]++;
  sum[cnt[i]]++;//出现次数为cnt[i]+1的数的个数+1
}

//缩小区间
void del(int i)
{
  sum[cnt[i]]--;
  cnt[i]--;
  sum[cnt[i]]++;
}

• 先减少原出现次数所在的数量，再增加新出现次数

• 注意：一开始 cnt[x] = 0，sum[0] 初始值可以认为是合法的

---

步骤 5：双指针执行所有查询

初始化 l = 1, r = 0，然后从空区间出发，依次执行每个查询：

  //左右边界，让区间一开始为空
  int l=1,r=0;
  //按顺序查询
  for(int i=1;i<=m;i++)
  {
    //左边界
    //扩展左边界
    //先移动边界再添加，否则会重复添加
    while(node[i].l<l) {add(nums[--l]);}
    //缩小左边界
    //先抛出当前的再移动边界
    while(node[i].l>l) {del(nums[l++]);}
    //右边界
    //扩展右边界
    while(node[i].r>r) {add(nums[++r]);}
    //缩小右边界
    while(node[i].r<r) {del(nums[r--]);}
    //放入答案
    ans[node[i].id]=sum[node[i].k];
  }

最终输出 ans[0..m-1] 即可

 

五、完整代码

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=1e5+10;
int n,m;
int len;
int sum[N];//恰好出现i次的数的个数
int cnt[N];//i在区间内出现的次数
int ans[N];
int nums[N];

//莫代算法
//查询结构体
//和查询有关的信息放在结构体中
struct Node
{
  int id;//原始序列号，方便输出的时候按照顺序
  int l,r,k;//区间边界值，出现k的次数
}node[N];

//查询结构体排序
bool cmp(const Node& a,const Node& b)
{
  //属于同一块，右端点小的优先
  if(a.l/len==b.l/len) return a.r<b.r;
  //否则，块小的优先
  else return a.l/len<b.l/len;
}

//扩展区间
void add(int i)
{
  sum[cnt[i]]--;//出现次数为cnt[i]的数的个数-1
  cnt[i]++;
  sum[cnt[i]]++;//出现次数为cnt[i]+1的数的个数+1
}

//缩小区间
void del(int i)
{
  sum[cnt[i]]--;
  cnt[i]--;
  sum[cnt[i]]++;
}

int main()
{
  cin>>n;
  len=sqrt(n);//莫代算法的块大小
  for(int i=1;i<=n;i++) cin>>nums[i];
  cin>>m;
  for(int i=1;i<=m;i++)
  {
    //存储查询结构体
    node[i].id=i;
    cin>>node[i].l>>node[i].r>>node[i].k;
  }
  //按照优先级对查询结构体排序
  sort(node+1,node+m+1,cmp);
  //左右边界，让区间一开始为空
  int l=1,r=0;
  //按顺序查询
  for(int i=1;i<=m;i++)
  {
    //左边界
    //扩展左边界
    //先移动边界再添加，否则会重复添加
    while(node[i].l<l) {add(nums[--l]);}
    //缩小左边界
    //先抛出当前的再移动边界
    while(node[i].l>l) {del(nums[l++]);}
    //右边界
    //扩展右边界
    while(node[i].r>r) {add(nums[++r]);}
    //缩小右边界
    while(node[i].r<r) {del(nums[r--]);}
    //放入答案
    ans[node[i].id]=sum[node[i].k];
  }
  //输出查询结果
  for(int i=1;i<=m;i++)
  {
    cout<<ans[i]<<endl;
  }
  return 0;
}

 

六、莫队算法知识点总结

关键词	说明
离线查询	所有查询可以提前读入
分块排序	按照左端点所在块、右端点排序
指针移动	l, r指针滑动调整当前区间
增量更新	利用 add 和 remove 操作高效维护答案
适用问题	频次统计、种类数、众数、贡献和等问题

 

七、总结

这道题的关键在于转化为区间频次统计问题，然后使用莫队进行优化，重要的需要掌握：

• 区间统计建模

• 莫队排序规则

• 增删函数的正确性