原文：annas-archive.org/md5/b306e51c73948c57f772d5af5f61eb39

译者：飞龙

协议：CC BY-NC-SA 4.0

第十一章：第二章

数据可视化

学习目标

本章结束时，您将能够：

  • 使用函数式方法创建和自定义折线图、条形图、直方图、散点图和箱线图

  • 开发程序化的、描述性的图表标题

  • 描述使用面向对象方法创建 Matplotlib 图表的优势

  • 创建一个包含单个轴或多个轴的可调用图表对象

  • 调整大小并保存包含多个子图的图表对象

  • 使用 Matplotlib 创建和自定义常见的图表类型。

本章将涵盖属于数据可视化范畴的各种概念。

简介

数据可视化是一种强大的工具，允许用户快速消化大量数据。有不同类型的图表用于各种目的。在业务中，折线图和条形图通常用于显示随时间变化的趋势和比较不同组之间的指标。而统计学家可能更感兴趣的是使用散点图或相关矩阵来检查变量之间的相关性。他们还可以使用直方图检查变量的分布或使用箱线图检查异常值。在政治中，饼图广泛用于比较不同类别之间的总数据。数据可视化可以非常复杂和创造性，仅限于个人的想象力。

Python 库 Matplotlib 是一个文档良好的二维绘图库，可以用来创建各种强大的数据可视化，其宗旨是“…让简单的事情变得简单，让困难的事情变得可能”（https://matplotlib.org/index.html）。

Matplotlib 创建图表的两种方法分别是函数式方法和面向对象方法。

在函数式方法中，创建一个包含单个图表的图形。通过一系列顺序函数来创建和自定义图表。但是，函数式方法不允许我们将图表保存到我们的环境中作为一个对象；这可以通过面向对象的方法实现。在面向对象的方法中，我们创建一个图形对象，为一个图表或多个子图分配一个轴或多个轴。然后，我们可以自定义轴或轴，并通过调用图形对象来调用单个图表或多个图表集合。

在本章中，我们将使用函数式方法来创建和自定义折线图、条形图、直方图、散点图和箱线图。然后，我们将学习如何使用面向对象的方法来创建和自定义单轴和多轴图。

函数式方法

在 Matplotlib 中使用函数式方法绘图是一种快速生成单轴图形的方式。通常，这是教给初学者的方法。函数式方法允许用户自定义并将图形保存为所选目录中的图像文件。在以下的练习和活动中，你将学习如何使用函数式方法绘制线形图、条形图、直方图、箱线图和散点图。

练习 13：函数式方法 – 线形图

要开始使用 Matplotlib，我们将从创建一个线形图开始，并对其进行自定义：

  1. 使用以下代码生成一个水平轴的数字数组，范围从 0 到 10，共 20 个均匀分布的值：

    import numpy as np
x = np.linspace(0, 10, 20)

  2. 创建一个数组并将其保存为对象y。以下代码片段将x的值立方并保存到数组y中：

    y = x**3

  3. 按如下方式创建图形：

    import matplotlib.pyplot as plt
plt.plot(x, y)
plt.show()

    参见这里的结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_01.jpg

    图 2.1：y 与 x 的线形图

  4. 使用以下代码添加一个 x 轴标签，内容为’Linearly Spaced Numbers’：

    plt.xlabel('Linearly Spaced Numbers')

  5. 使用以下代码添加一个 y 轴标签，内容为’y Value’：

    plt.ylabel('y Value')

  6. 使用以下代码添加一个标题，内容为’x by x cubed’：

    plt.title('x by x Cubed')

  7. 通过在plt.plot()函数中将颜色参数指定为k，将线条颜色更改为黑色：

    plt.plot(x, y, 'k')

    使用plt.show()将图形打印到控制台。

    查看以下截图，查看结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_02.jpg

    图 2.2：带有标签轴和黑色线条的线形图

  8. 将线条字符改为菱形；使用字符参数（即 D）结合颜色字符（即 k），如下所示：

    plt.plot(x, y, 'Dk')

    查看下图，查看结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_03.jpg

    图 2.3：带有未连接的黑色菱形标记的线形图

  9. 使用以下代码通过在D和k之间添加’-'来连接菱形，形成实线：

    plt.plot(x, y, 'D-k')

    参见下图查看输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_04.jpg

    图 2.4：带有连接的黑色菱形标记的线形图

  10. 使用plt.title()函数中的fontsize参数来增大标题的字体大小，如下所示：

    plt.title('x by x Cubed', fontsize=22)

  11. 使用以下代码将图形打印到控制台：

    plt.show()

  12. 输出可以在下图中看到：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_05.jpg

图 2.5：带有较大标题的线形图

在这里，我们使用函数式方法创建了一个单线的线形图，并对其进行了样式化，使其更具美感。然而，在同一个图中比较多个趋势并不罕见。因此，接下来的练习将详细讲解如何在同一线形图中绘制多条线并创建图例来区分这些线条。

练习 14：函数式方法 – 向线形图添加第二条线

Matplotlib 通过简单地指定另一个 plt.plot() 实例，使得在折线图中添加另一条线变得非常容易。在本练习中，我们将使用单独的线绘制 x 的立方和 x 的平方：

  1. 创建另一个 y 对象，就像我们为第一个 y 对象所做的那样，不过这次是对 x 进行平方，而不是立方，如下所示：

    y2 = x**2

  2. 现在，通过在现有图表中添加 plt.plot(x, y2)，将 y2 绘制在与 y 相同的图表上。

    参考此处的输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_06.jpg

    图 2.6：y 和 y2 随 x 的多条折线图

  3. 使用以下代码将 y2 的颜色更改为红色虚线：

    plt.plot(x, y2, '--r')

    输出显示在以下图示中：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_07.jpg

    图 2.7：y2 为红色虚线的多条折线图

  4. 要创建图例，我们必须首先使用 plt.plot() 函数中的 label 参数为我们的线条创建标签。

  5. 要将 y 标记为 ‘x 的立方’，使用以下代码：

    plt.plot(x, y, 'D-k', label='x cubed')

  6. 使用以下代码将 y2 标记为 ‘x 的平方’：

    plt.plot(x, y2, '--r', label='x squared')

  7. 使用 plt.legend(loc='upper left') 来指定图例的位置。

    请查看以下截图以查看最终输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_08.jpg

    图 2.8：带有图例的多条折线图

  8. 为了在新行开始时将一行文本分割成多行，我们使用字符串中的’\n’。因此，使用以下代码，我们可以创建此处显示的标题：

    plt.title('As x increases, \nx Cubed (black) increases \nat a Greater Rate than \nx Squared (red)', fontsize=22)

    请查看以下截图中的输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_09.jpg

    图 2.9：带有多行标题的多条折线图

  9. 要更改图表的尺寸，我们需要在 plt 实例的顶部添加 plt.figure(figsize=(10,5))。figsize 参数中的 10 和 5 分别指定了图表的宽度和高度。

    要查看输出，请参考以下图示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_10.jpg

图 2.10：增加图表尺寸的多条折线图

在本练习中，我们学习了如何使用函数式方法在 Matplotlib 中创建和设置单条和多条折线图。为了巩固我们的学习，我们将绘制另一张稍微不同样式的单条折线图。

活动 2：折线图

在本活动中，我们将创建一个折线图，分析从一月到六月每月销售商品的趋势。趋势将是正向的并且呈线性增长，并将使用带星形标记的蓝色虚线表示。x 轴将标记为 ‘月份’，y 轴将标记为 ‘销售商品数’。标题将显示为 ‘销售商品数呈线性增长：’

  1. 创建一个包含六个字符串的 x 列表，表示一月到六月的月份。

  2. 创建一个包含六个值的 y 列表，这些值表示 ‘销售商品数’，从 1000 开始，每个值增加 200，直到最后一个值为 2000。

  3. 生成上述描述的图表。

    查看以下截图以获取结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_11.jpg

图 2.11：按月份销售的商品线形图
注意

我们可以参考第 333 页的本活动解决方案。

到目前为止，我们已经获得了很多创建和自定义线形图的实践。线形图通常用于显示趋势。然而，在比较各组之间和/或组内的值时，条形图通常是首选的可视化方式。在接下来的练习中，我们将探讨如何创建条形图。

练习 15：创建条形图

在本练习中，我们将按商品类型显示销售收入：

  1. 创建一个商品类型的列表，并使用以下代码将其保存为 x：

    x = ['Shirts', 'Pants','Shorts','Shoes']

  2. 创建一个销售收入的列表，并按如下方式将其保存为 y：

    y = [1000, 1200, 800, 1800]

  3. 要创建条形图并将其打印到控制台，请参考以下代码：

    import matplotlib.pyplot as plt
plt.bar(x, y)
plt.show()

    以下截图显示了结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_12.jpg

    图 2.12：按商品类型划分的销售收入条形图

  4. 使用以下代码添加标题“Sales Revenue by Item Type”：

    plt.title('Sales Revenue by Item Type')

  5. 使用以下代码创建一个显示“Item Type”的 x 轴标签：

    plt.xlabel('Item Type')

  6. 使用以下代码添加一个 y 轴标签，显示“Sales Revenue ($)”：

    plt.ylabel('Sales Revenue ($)')

    以下截图显示了输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_13.jpg

    图 2.13：带有自定义轴和标题的条形图

  7. 我们将创建一个标题，该标题会根据绘制的数据进行更改。对于这个示例，标题将是“Shoes Produce the Most Sales Revenue”。首先，我们将找到 y 中最大值的索引，并使用以下代码将其保存为 index_of_max_y 对象：

    index_of_max_y = y.index(max(y))

  8. 使用以下代码，将列表 x 中与 index_of_max_y 索引相等的项保存到 most_sold_item 对象：

    most_sold_item = x[index_of_max_y]

  9. 按照以下方式使标题具有程序化功能：

    plt.title('{} Produce the Most Sales Revenue'.format(most_sold_item))

    查看以下输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_14.jpg

    图 2.14：带有程序化标题的条形图

  10. 如果我们希望将图表转换为水平条形图，可以通过将 plt.bar(x, y) 替换为 plt.barh(x, y) 来实现。

    以下截图显示了输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_15.jpg

    图 2.15：带有错误标注轴的水平条形图
    注意

    记住，当条形图从垂直转为水平时，x 轴和 y 轴需要互换。

  11. 将 x 和 y 的标签分别从 plt.xlabel('Item Type') 和 plt.ylabel('Sales Revenue ($)') 互换为 plt.xlabel('Sales Revenue ($)') 和 plt.ylabel('Item Type')。

查看以下输出，获取最终的条形图：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_16.jpg

图 2.16：带有正确标注轴的水平条形图

在前一个练习中，我们学习了如何创建条形图。使用 Matplotlib 创建条形图非常简单。在接下来的活动中，我们将继续练习构建条形图。

活动 3：条形图

在本活动中，我们将创建一个条形图，比较五支获得最多冠军头衔的 NBA 球队的冠军数量。该图将按标题数从大到小排序，拥有最多头衔的球队在左侧，最少的在右侧。柱状条将为红色，x 轴将命名为 ‘NBA 球队’，y 轴将命名为 ‘冠军数量’，标题将是程序化的，解释哪支球队拥有最多冠军及其数量。在进行此活动之前，请确保在线查找所需的 NBA 球队数据。此外，我们将使用 plt.xticks(rotation=45) 将 x 轴刻度标签旋转 45 度，以避免重叠，并将图表保存到当前目录：

  1. 为 x 创建一个包含五个字符串的列表，这些字符串是获得最多冠军头衔的 NBA 球队名称。

  2. 为 y 创建一个包含五个值的列表，这些值对应于 x 中的字符串，表示 ‘获得的冠军头衔’。

  3. 将 x 和 y 放入一个数据框，其中列名分别为 ‘队伍’ 和 ‘冠军头衔’。

  4. 按 ‘标题’ 进行降序排序数据框。

  5. 创建一个程序化的标题并将其保存为 title。

  6. 生成描述的图形。

    注意

    我们可以参考第 334 页的解答来完成此活动。

折线图和条形图是两种非常常见且有效的可视化方式，分别用于报告趋势和比较不同组。然而，若要进行更深入的统计分析，生成能揭示特征特性（而这些特征在折线图和条形图中无法显现）的图形就显得尤为重要。因此，在接下来的练习中，我们将学习创建常见的统计图表。

练习 16：函数式方法 – 直方图

在统计学中，在进行任何类型的分析之前，了解连续变量的分布是非常重要的。为了展示分布，我们将使用直方图。直方图通过给定数组的区间显示频率：

  1. 为了展示如何创建直方图，我们将生成一个包含 100 个符合正态分布的值的数组，均值为 0，标准差为 0.1，并使用以下代码将其保存为 y：

    import numpy as np
y = np.random.normal(loc=0, scale=0.1, size=100)

  2. 导入 Matplotlib 后，使用以下代码创建直方图：

    plt.hist(y, bins=20)

  3. 使用以下代码为 x 轴创建一个名为 ‘y 值’ 的标签：

    plt.xlabel('y Value')

  4. 使用以下代码将 y 轴命名为 ‘频率’：

    plt.ylabel('Frequency')

  5. 使用 plt.show() 将其打印到控制台：

  6. 查看以下截图中的输出：https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_17.jpg

    图 2.17：带有标注坐标轴的 y 直方图
    注意

    当我们查看直方图时，我们通常会判断分布是否为正态分布。有时，一个分布看起来是正态分布，但实际上不是；而有时，一个分布看起来不是正态分布，但实际上是正态的。为了检测正态性，有一个叫做 Shapiro-Wilk 检验的方法。Shapiro-Wilk 检验的原假设是数据是正态分布的。因此，p 值 < 0.05 表示非正态分布，而 p 值 > 0.05 表示正态分布。我们将使用 Shapiro-Wilk 检验的结果来创建一个程序化标题，告知读者分布是否为正态分布。

  7. 使用元组解包，将 Shapiro-Wilk 检验中的 W 统计量和 p 值分别保存到shap_w和shap_p对象中，代码如下：

    from scipy.stats import shapiro
shap_w, shap_p = shapiro(y)

  8. 我们将使用 if-else 语句来判断数据是否为正态分布，并将适当的字符串存储在normal_YN对象中。

    if shap_p > 0.05:
    normal_YN = 'Fail to reject the null hypothesis. Data is normally distributed.'
else:
    normal_YN = 'Null hypothesis is rejected. Data is not normally distributed.'

  9. 使用plt.title(normal_YN)将normal_YN赋值给我们的图表，并使用plt.show()将其打印到控制台。

    请查看此截图中的最终输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_18.jpg

图 2.18：带有程序化标题的 y 的直方图

如前所述，直方图用于显示数组的分布。另一个常用的统计图表用于探索数值特征的是箱线图，也称为箱型图。

箱线图显示了一个数组的分布，基于最小值、第一个四分位数、中位数、第三个四分位数和最大值，但它们主要用于表示分布的偏斜程度并识别离群值。

练习 17：函数式方法 – 箱线图

在本练习中，我们将学习如何创建箱线图，并在标题中呈现关于分布形状和离群值数量的信息：

  1. 使用以下代码生成一个均值为 0，标准差为 0.1 的 100 个正态分布的数字数组，并将其保存为 y：

    import numpy as np
y = np.random.normal(loc=0, scale=0.1, size=100)

  2. 如下创建并显示图表：

    import matplotlib.pyplot as plt
plt.boxplot(y) 
plt.show()

    有关输出，请参见下图：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_19.jpg

    图 2.19：y 的箱线图
    注意

    该图显示了一个框，表示四分位距（IQR）。框的顶部是第 25 百分位（即 Q1），框的底部是第 75 百分位（即 Q3）。穿过盒子的橙色线是中位数。框上方和下方延伸的两条线是“胡须”。上胡须的顶部是“最大”值，通过 Q1 - 1.5IQR 计算得出。下胡须的底部是“最小”值，通过 Q3 + 1.5IQR 计算得出。离群值（或边缘离群值）以点的形式显示在“最大”胡须上方或“最小”胡须下方。

  3. 使用以下代码将 Shapiro W 和 p 值从shapiro函数保存：

    from scipy.stats import shapiro
shap_w, shap_p = shapiro(y)

  4. 参考以下代码将y转换为 z 得分：

    from scipy.stats import zscore
y_z_scores = zscore(y)
    注意

    这是衡量数据的一种方式，显示每个数据点与均值的标准差差异。

  5. 使用以下代码迭代 y_z_scores 数组，以找到离群值的数量：

    total_outliers = 0 
for i in range(len(y_z_scores)): 
    if abs(y_z_scores[i]) >= 3:
        total_outliers += 1
    注释

    由于生成的数组 y 是正态分布的，因此我们可以预期数据中没有离群值。

  6. 生成一个标题，传达数据是否呈正态分布，以及离群值的数量。如果 shap_p 大于 0.05，则我们的数据呈正态分布。如果小于 0.05，则数据不呈正态分布。我们可以通过以下逻辑设置并包含离群值的数量：

    if shap_p > 0.05:
    title = 'Normally distributed with {} outlier(s).'.format(total_outliers)
else:
    title = 'Not normally distributed with {} outlier(s).'.format(total_outliers)

  7. 使用 plt.title（标题）设置我们的图表标题，并通过以下方式打印到控制台：

    plt.show()

  8. 在下图中检查最终输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_20.jpg

图 2.20：带程序生成标题的 y 的箱线图

直方图和箱线图在探索数值数组特征时非常有效。然而，它们并不能提供数组之间关系的信息。在下一个练习中，我们将学习如何创建散点图——一种常见的可视化方式，用于展示两个连续数组之间的关系。

练习 18：散点图

在本练习中，我们将创建一个体重与身高的散点图。我们将再次创建一个标题来解释该图所展示的信息：

  1. 使用以下方法生成一个表示身高的数字列表，并将其保存为 y：

    y = [5, 5.5, 5, 5.5, 6, 6.5, 6, 6.5, 7, 5.5, 5.25, 6, 5.25]

  2. 使用以下方法生成一个表示体重的数字列表，并将其保存为 x：

    x = [100, 150, 110, 140, 140, 170, 168, 165, 180, 125, 115, 155, 135]

  3. 使用以下代码创建一个基本的散点图，体重为 x 轴，身高为 y 轴：

    import matplotlib.pyplot as plt
plt.scatter(x, y)

  4. 将 x 轴标记为 ‘体重’，如下所示：

    plt.xlabel('Weight')

  5. 将 y 轴标记为 ‘身高’，如下所示：

    plt.ylabel('Height')

  6. 使用 plt.show() 将图表打印到控制台。

    我们的输出应类似于以下内容：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_21.jpg

    图 2.21：按体重绘制的身高散点图

  7. 我们希望图表标题能告知读者关系的强度和 Pearson 相关系数。因此，我们将计算 Pearson 相关系数，并在标题中解释该系数的值。计算 Pearson 相关系数的代码如下：

    from scipy.stats import pearsonr
correlation_coeff, p_value = pearsonr(x, y)

  8. Pearson 相关系数是一个指标，用于衡量两个连续数组之间线性关系的强度和方向。使用 if-else 逻辑，我们将通过以下代码返回相关系数的解释：

    if correlation_coeff == 1.00:
    title = 'There is a perfect positive linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff >= 0.8:
    title = 'There is a very strong, positive linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff >= 0.6:
    title = 'There is a strong, positive linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff >= 0.4:
    title = 'There is a moderate, positive linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff >= 0.2:
    title = 'There is a weak, positive linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff > 0:
    title = 'There is a very weak, positive linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff == 0:
    title = 'There is no linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff <= -0.8:
    title = 'There is a very strong, negative linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff <= -0.6:
    title = 'There is a strong, negative linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff <= -0.4:
    title = 'There is a moderate, negative linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
elif correlation_coeff <= -0.2:
    title = 'There is a weak, negative linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
else: 
    title = 'There is a very weak, negative linear relationship (r = {0:0.2f}).'.format(correlation_coeff)
print(title)

  9. 现在，我们可以使用新创建的标题对象作为标题，方法是使用 plt.title(title)。

    请参阅下图以了解结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_22.jpg

图 2.22：按体重绘制的身高散点图，带程序生成的标题

到目前为止，我们已经学习了如何使用函数式方法为不同目的创建和设置各种图表样式。虽然这种绘图方法非常有效，可以快速生成可视化图表，但它无法创建多个子图，也无法将图表保存为我们环境中的对象。为了将图表保存为对象，我们必须使用面向对象的方法，这将在接下来的练习和活动中进行介绍。

使用子图的面向对象方法

使用 Matplotlib 的函数式绘图方法不允许用户将图表保存为我们环境中的对象。在面向对象的方法中，我们创建一个图形对象，作为一个空画布，然后我们将一组坐标轴或子图添加到图形中。该图形对象是可调用的，如果被调用，将返回该图形到控制台。我们将通过绘制与练习 13中相同的 x 和 y 对象来演示这一过程。

练习 19：使用子图绘制单条线

当我们学习 Matplotlib 的函数式绘图方法时，我们从创建和自定义一条线性图开始。在本次练习中，我们将使用函数式绘图方法创建并设置样式的线性图：

  1. 使用以下代码将x保存为从 0 到 10 的数组，间隔为 20 个线性步长：

    import numpy as np
x = np.linspace(0, 10, 20)

    使用以下代码将y保存为 x 的三次方：

    y = x**3

  2. 按以下步骤创建图形和坐标轴：

    import matplotlib.pyplot as plt 
fig, axes = plt.subplots() 
plt.show()

    查看以下屏幕截图以查看输出结果：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_23.jpg

    图 2.23：可调用的图形和坐标轴集
    注意

    fig对象现在是可调用的，并返回我们可以绘制的坐标轴。

  3. 使用以下代码绘制 y（即 x 的平方）与 x 的关系：

    axes.plot(x, y)

    下图显示了输出结果：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_24.jpg

    图 2.24：按 x 绘制 y 的可调用线性图

  4. 将图表样式设置与练习 13中的样式相同。首先，按照以下步骤更改线条颜色和标记：

    axes.plot(x, y, 'D-k')

  5. 使用以下代码将 x 轴标签设置为’线性间隔数字’：

    axes.set_xlabel('Linearly Spaced Numbers')

  6. 使用以下代码将 y 轴设置为’y 值’：

    axes.set_ylabel('y Value')

  7. 使用以下代码将标题设置为’随着 x 的增加，y 按 x 的三次方增加’：

    axes.set_title('As x increases, y increases by x cubed')

    下图显示了输出结果：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_25.jpg

图 2.25：按 x 绘制 y 的可调用样式线图

在本次练习中，我们创建了一个与练习 13中的第一个图表非常相似的图表，但现在它是一个可调用的对象。使用面向对象的绘图方法的另一个优势是可以在单个图形对象上创建多个子图。

在某些情况下，我们希望并排比较不同的数据视图。我们可以在 Matplotlib 中使用子图来实现这一点。

练习 20：使用子图绘制多条线

因此，在本练习中，我们将绘制与练习 14 中相同的线条，但我们将在同一个可调用的图形对象中绘制两个子图。子图是通过网格格式布局的，并可以通过 [行，列] 索引访问。例如，如果我们的图形对象包含四个子图，排列成两行两列，我们可以通过 axes[0,0] 引用左上角的图形，使用 axes[1,1] 引用右下角的图形，如下图所示。

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_26.jpg

图 2.26：坐标轴索引引用

在剩余的练习和活动中，我们将有很多机会练习生成子图并访问各种坐标轴。在本练习中，我们将使用子图绘制多个线图：

  1. 首先，使用以下代码创建 x、y 和 y2：

    import numpy as np
x = np.linspace(0, 10, 20)
y = x**3
y2 = x**2

  2. 创建一个包含两个坐标轴（即子图）的图像，它们并排显示（即 1 行 2 列），如下所示：

    import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=2)

    结果输出如下所示：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_27.jpg

    图 2.27：包含两个子图的图像

  3. 要访问左侧的子图，请将其引用为 axes[0]。要访问右侧的图形，请将其引用为 axes[1]。在左侧坐标轴上，使用以下代码绘制 y 对 x 的图像：

    axes[0].plot(x, y)

  4. 使用以下内容添加标题：

    axes[0].set_title('x by x Cubed')

  5. 使用以下代码行生成 x 轴标签：

    axes[0].set_xlabel('Linearly Spaced Numbers')

  6. 使用以下代码创建 y 轴标签：

    axes[0].set_ylabel('y Value')

    结果输出如下所示：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_28.jpg

    图 2.28：包含两个子图的图像，左侧已创建

  7. 在右侧坐标轴上，使用以下代码绘制 y2 对 x 的图像：

    axes[1].plot(x, y2)

  8. 使用以下代码添加标题：

    axes[1].set_title('x by x Squared')

  9. 使用以下代码生成 x 轴标签：

    axes[1].set_xlabel('Linearly Spaced Numbers')

  10. 使用以下代码创建 y 轴标签：

    axes[1].set_ylabel('y Value')

    以下截图显示了输出结果：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_29.jpg

    图 2.29：包含两个子图的图像

  11. 我们已经成功创建了两个子图。然而，看起来右侧的图的 y 轴与左侧图重叠。为了防止图形重叠，可以使用 plt.tight_layout()。

    这里显示的是输出结果：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_30.jpg

图 2.30：包含两个不重叠子图的图像

使用面向对象的方法，我们只需调用 fig 对象即可显示两个子图。我们将在活动 4 中进一步练习面向对象的绘图方法。

活动 4：使用子图绘制多种图类型

到目前为止，我们已经学习了如何使用函数式方法构建、定制和编程线性图、条形图、直方图、散点图和箱形图。在第 19 个练习中，我们介绍了面向对象的方法，而在第 20 个练习中，我们学习了如何使用子图创建包含多个图的图形。因此，在本活动中，我们将利用子图创建一个包含多个图表和图表类型的图形。我们将创建一个包含六个子图的图形。子图将按三行两列的布局显示（见图 2.31）：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_31.jpg

](https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_31.jpg)

图 2.31：子图布局

一旦我们生成了六个子图的图形，我们可以通过’行，列’索引访问每个子图（见图 2.32）：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_02_32.jpg

图 2.32：坐标轴索引引用

因此，要访问线性图（即左上角），使用axes[0, 0]。要访问直方图（即中右），使用axes[1, 1]。我们将在接下来的活动中练习这一点：

  1. 从 GitHub 导入’Items_Sold_by_Week.csv’和’Weight_by_Height.csv’，并生成一个符合正态分布的数字数组。

  2. 生成一个包含六个空子图的图形，使用三行两列的布局，确保子图不重叠。

  3. 设置图形标题，确保六个子图排列成三行两列且不重叠。

  4. 在’Line’、'Bar’和’Horizontal Bar’坐标轴上，使用’Items_Sold_by_Week.csv’绘制按’Week’排序的’Items_Sold’数据。

  5. 在’Histogram’和’Box-and-Whisker’坐标轴上，绘制包含 100 个符合正态分布的数字的数组。

  6. 在’Scatter’坐标轴上，使用’Weight_by_Height.csv’绘制按身高排序的体重图。

  7. 为每个子图标注 x 轴和 y 轴。

  8. 增加图形的大小并保存。

    注意

    本活动的解决方案可以在第 338 页找到。

总结

在本章中，我们使用了 Python 绘图库 Matplotlib 来创建、定制和保存图表，采用了函数式方法。然后，我们讲解了描述性标题的重要性，并创建了我们自己的描述性编程标题。然而，函数式方法并不创建可调用的图形对象，也不返回子图。因此，为了创建一个可调用的图形对象并能够包含多个子图，我们采用了面向对象的方法来创建、定制和保存图表。绘图需求因分析而异，因此在本章中覆盖所有可能的图表并不实际。为了创建满足每个分析需求的强大图表，熟悉 Matplotlib 文档页面中的文档和示例至关重要。

在下一章中，我们将应用一些这些绘图技巧，进入使用 scikit-learn 的机器学习部分。

第十章. 数据分析的未来及技能发展方向

“我们正在创建和招聘以填补‘新领衔’职位——这些完全是新的职位，涉及如网络安全、数据科学、人工智能和认知商业等领域。”

– Ginni Rometty，IBM 董事长兼首席执行官

再次感谢并祝贺你，亲爱的读者，完成了这些长篇章节的阅读，并且可能尝试了一些或所有提供的示例代码。我尽力在深入探讨某个特定主题（例如深度学习或时间序列分析）的基础上，提供给实际操作人员的综合示例代码之间找到一个良好的平衡。我特别希望你能发现将数据科学分析与 PixieApp 应用编程模型紧密集成到一个 Jupyter Notebook 中的想法既有趣又新颖。但最重要的是，我希望你觉得它是有用的，并且是你可以在自己的项目和团队中重用的内容。

在第一章 编程与数据科学 – 新工具集的开头，我使用了 Drew 的 Conway 数据科学韦恩图（这是我最喜欢的图表之一）来表示什么是数据科学，以及为什么数据科学家通常被认为是独角兽。虽然我非常尊重 Drew Conway，但我想扩展这个图表，以表明开发者在数据科学领域中日益重要和不断增长的角色，如下图所示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/B09699_10_01.jpg

Drew 的 Conway 数据科学韦恩图，现在包括了开发者

我现在想利用最后一章来提供我对未来的看法，以及在人工智能和数据科学方面的预期。

前瞻性思维——人工智能和数据科学的未来预期

这一部分我非常喜欢，因为我可以表达前瞻性的观点，而不必为其准确性负责，因为从定义上讲，这些只是我的个人观点！前瞻性思维——人工智能和数据科学的未来预期。

正如我在第一章 编程与数据科学 – 新工具集中所解释的那样，我相信人工智能和数据科学将会持续存在，并且它们将在可预见的未来继续对现有行业产生颠覆性影响，最可能以加速的速度进行。这无疑会影响到总体的就业数量，类似于我们过去所见过的其他技术革命（农业革命、工业革命、信息革命等），一些岗位将会消失，而新的岗位也将被创造出来。

2016 年，IBM 董事长兼首席执行官 Ginny Rometty 在给唐纳德·特朗普总统的信中（www.ibm.com/blogs/policy/ibm-ceo-ginni-romettys-letter-u-s-president-elect）谈到了通过创造她所称之为“新领带”类型的工作，来更好地为人工智能革命做准备，以下是信中的一段摘录：

“在今天的 IBM 找到一份工作并不总是需要大学学位；在我们美国的部分中心，甚至有三分之一的员工没有四年制大学学位。最重要的是相关技能，有时这些技能是通过职业培训获得的。此外，我们还在创造和招聘‘新领带’岗位——全新的角色，涵盖网络安全、数据科学、人工智能和认知业务等领域。”

这些“新领带”工作只有在我们成功实现数据科学的民主化时才能大规模创造，因为数据科学是人工智能的生命线，每个人都需要在某种程度上参与其中；开发人员、业务线用户、数据工程师等等。可以想象，这些新型工作的需求将如此之高，以至于传统的学术轨道将无法满足这些需求。相反，行业将负有责任通过创建新项目来填补这一空白，这些项目旨在重新培训所有那些工作可能面临被淘汰风险的现有员工。像苹果的人人都能编程项目（www.apple.com/everyone-can-code）这样的新项目将会涌现；也许会有类似任何人都能做数据科学的项目。我还认为，MOOCs（即大规模在线开放课程）将在未来扮演更加重要的角色，正如我们今天已经看到的，Coursera 和 edX 等主要 MOOC 平台与 IBM 等公司之间的合作伙伴关系越来越多（见www.coursera.org/ibm）。

公司还可以做其他事情，以更好地为人工智能和数据科学革命做好准备。在第一章，编程与数据科学——一种新的工具集中，我谈到了可以帮助我们实现这一雄心壮志目标的数据科学战略的三大支柱：数据、服务和工具。

在服务方面，公共云的高速增长大大推动了多个领域内高质量服务的整体提升：数据持久化、认知、流媒体等等。像亚马逊、Facebook、谷歌、IBM 和微软等提供商正引领着基于强大平台的服务优先的创新能力建设，为开发人员提供一致的体验。这一趋势将继续加速，越来越多强大的服务将在越来越快的速度下发布。

一个很好的例子是谷歌的自学习 AI——AlphaZero（en.wikipedia.org/wiki/AlphaZero），它在 4 小时内自学会了国际象棋，并最终打败了一款冠军象棋程序。另一个很好的例子来自 IBM 最近宣布的项目辩论者（www.research.ibm.com/artificial-intelligence/project-debater），它是第一个可以与人类在复杂话题上辩论的 AI 系统。这些类型的进展将持续推动越来越强大的服务的可用性，这些服务可以被包括开发者在内的每个人访问。聊天机器人是另一个成功实现民主化的服务示例，开发者现在比以往任何时候都更容易创建具有对话能力的应用程序。我相信，随着时间的推移，消费这些服务将变得越来越容易，从而使开发者能够构建我们今天甚至无法想象的令人惊叹的新应用程序。

在数据方面，我们需要使访问高质量数据变得比现在更容易。我想到的一个模型来自一部叫做24 小时的电视剧。完全坦白；我喜欢看电视剧并且狂看一整季，我认为其中一些电视剧能很好地反映技术的发展方向。在24 小时中，反恐特工杰克·鲍尔有 24 小时的时间阻止坏人制造灾难性事件。看这部剧时，我总是对数据如何轻松地从指挥中心的分析员传输到杰克·鲍尔的手机感到惊讶，或者当数据问题只有几分钟时间来解决时，分析员如何能从不同的系统（卫星图像、记录系统等）中召唤数据，精准锁定坏人；例如，我们正在寻找在过去两个月内购买过这种化学品并且位于某个特定半径范围内的人。哇！从我的角度看，这就是数据科学家访问和处理数据应该是如此简单和无摩擦的过程。我相信，我们正朝着这个目标取得巨大进展，工具如 Jupyter Notebooks 正充当着连接数据源与服务和分析的控制平面。Jupyter Notebooks 将工具带到数据面前，而不是相反，从而大大降低了任何希望参与数据科学的人的入门成本。

参考文献

附录 A. PixieApp 快速参考

本附录是开发者的快速参考指南，提供了所有 PixieApp 属性的汇总。

注解

  • @PixieApp：类注解，必须添加到任何 PixieApp 类上。

    参数：无

    示例：

    from pixiedust.display.app import *
@PixieApp
class MyApp():
    pass

  • @route：方法注解，必须加到一个方法上，以表示该方法（方法名可以随意）与一个路由相关联。

    参数：**kwargs。表示路由定义的关键字参数（键值对）。PixieApp 调度程序会根据以下规则将当前内核请求与路由进行匹配：

    • 参数数量最多的路由将最先被评估。

    • 所有参数必须匹配，路由才会被选中。参数值可以使用 * 来表示匹配任何值。

    • 如果找不到路由，则会选择默认路由（没有参数的那个）。

    • 路由参数的每个键可以是临时状态（由 pd_options 属性定义）或持久化状态（PixieApp 类的字段，直到明确更改之前都会保留）。

    • 方法可以有任意数量的参数。在调用方法时，PixieApp 调度程序将尝试根据参数名将方法参数与路由参数进行匹配。

    返回值：该方法必须返回一个 HTML 片段（除非使用了 @captureOutput 注解），该片段将被注入到前端。方法可以利用 Jinja2 模板语法生成 HTML。HTML 模板可以访问一些特定的变量：

    • this：引用 PixieApp 类（注意，我们使用 this 而不是 self，因为 self 已经被 Jinja2 框架本身使用）

    • prefix：一个字符串 ID，唯一标识 PixieApp 实例

    • entity：请求的当前数据实体

    • 方法参数：方法的所有参数都可以作为变量在 Jinja2 模板中访问。

      from pixiedust.display.app import *
@PixieApp
class MyApp():
    @route(key1=”value1”, key2=”*”)
    def myroute_screen(self, key1, key2):
        return “<div>fragment: Key1 = {{key1}} - Key2 = {{key2}}”

    示例：

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode25.py

  • @templateArgs：注解，允许在 Jinja2 模板中使用任何本地变量。注意，@templateArgs 不能与 @captureOutput 一起使用：

    参数：无

    示例：

    from pixiedust.display.app import *
@PixieApp
class MyApp():
    @route(key1=”value1”, key2=”*”)
    @templateArgs
    def myroute_screen(self, key1, key2):
        local_var = “some value”
        return “<div>fragment: local_var = {{local_var}}”

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode26.py

  • @captureOutput：注解用于改变路由方法的契约，使得方法不再需要返回 HTML 片段。相反，方法体可以像在 Notebook 单元中那样直接输出结果。框架会捕获输出并以 HTML 形式返回。注意，在这种情况下你不能使用 Jinja2 模板。

    参数：无

    示例：

    from pixiedust.display.app import *
import matplotlib.pyplot as plt
@PixieApp
class MyApp():
    @route()
    @captureOutput
    def main_screen(self):
        plt.plot([1,2,3,4])
        plt.show()

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode27.py

  • @Logger：通过向类添加日志方法来添加日志功能：debug、warn、info、error、critical、exception。

    参数：无

    示例：

    from pixiedust.display.app import *
from pixiedust.utils import Logger
@PixieApp
@Logger()
class MyApp():
    @route()
    def main_screen(self):
        self.debug(“In main_screen”)
        return “<div>Hello World</div>”

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode28.py

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode28.py

自定义 HTML 属性

这些可以与任何常规 HTML 元素一起使用，用于配置内核请求。当元素接收到点击或更改事件时，或者在 HTML 片段完成加载后，PixieApp 框架可以触发这些请求。

  • pd_options：定义内核请求瞬态状态的键值对列表，格式如下：pd_options=”key1=value1;key2=value2;...”。当与pd_entity属性结合使用时，pd_options属性会调用 PixieDust 的display() API。在这种情况下，你可以从另一个 Notebook 单元格的元数据中获取值，在该单元格中你已经使用了display() API。建议在display()模式下使用pd_options时，为了方便起见，可以通过创建一个名为<pd_options>的子元素，并将 JSON 值作为文本包含在其中，来使用pd_options的 JSON 表示法。

    使用pd_options作为子元素调用display()的示例：

    <div pd_entity>
    <pd_options>
        {
            “mapboxtoken”: “XXXXX”,
            “chartsize”: “90”,
            “aggregation”: “SUM”,
            “rowCount”: “500”,
            “handlerId”: “mapView”,
            “rendererId”: “mapbox”,
            “valueFields”: “IncidntNum”,
            “keyFields”: “X,Y”,
            “basemap”: “light-v9”
        }
    </pd_options>
</div>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode29.html

    使用pd_options作为 HTML 属性的示例：

    <!-- Invoke a route that displays a chart -->
<button type=”submit” pd_options=”showChart=true” pd_target=”chart{{prefix}}”>
    Show Chart
</button>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode30.html

  • pd_entity：仅用于在特定数据上调用display() API。必须与pd_options一起使用，其中的键值对将作为参数传递给display()。如果没有为pd_entity属性指定值，则假定它是传递给启动 PixieApp 的run方法的实体。pd_entity的值可以是 Notebook 中定义的变量，也可以是 PixieApp 的字段（例如，pd_entity=”df”），或者是使用点符号表示法指向对象的字段（例如，pd_entity=”obj_instance.df”）。

  • pd_target：默认情况下，内核请求的输出会被注入到整体输出单元格或对话框中（如果你将runInDialog="true"作为run方法的参数）。但是，你可以使用pd_target="elementId"来指定一个接收输出的目标元素。（请注意，elementId必须在当前视图中存在。）

    示例：

    <div id=”chart{{prefix}}”>
<button type=”submit” pd_options=”showChart=true” pd_target=”chart{{prefix}}”>
    Show Chart
</button>
</div>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode31.html

  • pd_script：此属性调用任意的 Python 代码作为内核请求的一部分。可以与其他属性如pd_entity和pd_options结合使用。需要注意的是，必须遵守 Python 的缩进规则（docs.python.org/2.0/ref/indentation.html），以避免运行时错误。

    如果 Python 代码包含多行，建议将pd_script作为子元素使用，并将代码存储为文本。

    示例：

    <!-- Invoke a method to load a dataframe before visualizing it -->
<div id=”chart{{prefix}}”>
<button type=”submit”
    pd_entity=”df”
    pd_script=”self.df = self.load_df()”
    pd_options=”handlerId=dataframe”
    pd_target=”chart{{prefix}}”>
    Show Chart
</button>
</div>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode32.html

  • pd_app：此属性通过其完全限定类名动态调用一个独立的 PixieApp。可以使用pd_options属性传递路由参数，以调用 PixieApp 的特定路由。

    示例：

    <div pd_render_onload
     pd_option=”show_route_X=true”
     pd_app=”some.package.RemoteApp”>
</div>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode33.html

  • pd_render_onload：此属性应在页面加载时触发内核请求，而不是在用户点击某个元素或发生变化事件时触发。pd_render_onload属性可以与定义请求的其他属性结合使用，如pd_options或pd_script。请注意，此属性只能与 div 元素一起使用。

    示例：

    <div pd_render_onload>
    <pd_script>
print(‘hello world rendered on load’)
    </pd_script>
</div>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode34.html

  • pd_refresh：此属性用于强制 HTML 元素执行内核请求，即使没有发生任何事件（点击或变化事件）。如果没有指定值，则刷新当前元素；否则，刷新值中指定 ID 的元素。

    示例：

    <!-- Update state before refreshing a chart -->
<button type=”submit”
    pd_script=”self.show_line_chart()”
    pd_refresh=”chart{{prefix}}”>
    Show line chart
</button>

    注意

    你可以在这里找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode35.html

  • pd_event_payload：此属性用于发出一个带有指定负载内容的 PixieApp 事件。该属性遵循与pd_options相同的规则：

    • 每个键值对必须使用key=value表示法进行编码

    • 事件将在点击或变化事件时触发

    • 支持使用$val()指令动态注入用户输入

    • 使用<pd_event_payload>子元素输入原始 JSON。

      <button type=”submit” pd_event_payload=”type=topicA;message=Button clicked”>
    Send event A
</button>
<button type=”submit”>
    <pd_event_payload>
    {
        “type”:”topicA”,
        “message”:”Button Clicked”
    }
    </pd_event_payload>
    Send event A
</button>

    示例：

    注意

    你可以在此处找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode36.html

  • pd_event_handler：订阅者可以通过声明<pd_event_handler>子元素来监听事件，该元素可以接受任何 PixieApp 内核执行属性，如pd_options和pd_script。该元素必须使用pd_source属性来过滤其想要处理的事件。pd_source属性可以包含以下值之一：

    • targetDivId：只有来自指定 ID 元素的事件才会被接受

    • type：只有指定类型的事件才会被接受

      <div class=”col-sm-6” id=”listenerA{{prefix}}”>
    Listening to button event
    <pd_event_handler
        pd_source=”topicA”
        pd_script=”print(eventInfo)”
        pd_target=”listenerA{{prefix}}”>
    </pd_event_handler>
</div>

    示例：

    注意

    你可以在此处找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode37.html

    注意：使用*作为pd_source表示将接受所有事件。

  • pd_refresh_rate：用于在指定的时间间隔内（以毫秒为单位）重复执行一个元素。这对于需要轮询特定变量状态并在 UI 中显示结果的场景非常有用。

    示例：

    <div pd_refresh_rate=”3000”
    pd_script=”print(self.get_status())”>
</div>

    注意

    你可以在此处找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode38.html

方法

  • setup：这是 PixieApp 实现的可选方法，用于初始化其状态。在 PixieApp 运行之前会自动调用。

    参数：无

    示例：

    def setup(self):
    self.var1 = “some initial value”
    self.pandas_dataframe = pandas.DataFrame(data)

    注意

    你可以在此处找到代码文件：

    github.com/DTAIEB/Thoughtful-Data-Science/blob/master/chapter%205/sampleCode39.py

  • run：用于启动 PixieApp。

    参数：

    • 实体：[可选] 作为输入传递给 PixieApp 的数据集。可以通过pd_entity属性或直接作为名为pixieapp_entity的字段引用。

    • **kwargs：要传递给 PixieApp 的关键字参数。例如，使用runInDialog="true"将以对话框方式启动 PixieApp。

      app = MyPixieApp()
app.run(runInDialog=”true”)

    示例：

  • invoke_route：用于以编程方式调用路由。

    参数：

    • 路由方法：需要调用的方法。

    • **kwargs：要传递给路由方法的关键字参数。

      app.invoke_route(app.route_method, arg1 = “value1”, arg2 = “value2”)

    示例：

  • getPixieAppEntity：用于检索调用run()方法时传递的当前 PixieApp 实体（可能为 None）。getPixieAppEntity()通常在 PixieApp 内部调用，即：

    self.getPixieAppEntity()

第十三章：第三章

通过 Scikit-Learn 进行机器学习简介

学习目标

本章结束时，你将能够：

  • 为不同类型的有监督学习模型准备数据。

  • 使用网格搜索调整模型的超参数。

  • 从调整过的模型中提取特征重要性。

  • 评估分类和回归模型的表现。

在本章中，我们将讲解处理数据并使数据准备好进行分析的关键概念。

介绍

scikit-learn 是一个免费的开源库，专为 Python 构建，包含一系列有监督和无监督的机器学习算法。此外，scikit-learn 提供数据预处理、超参数调优和模型评估的功能，我们将在接下来的章节中涉及到这些内容。它简化了模型构建过程，并且易于在各种平台上安装。scikit-learn 起步于 2007 年，由 David Corneapeau 在 Google Summer of Code 项目中创建，经过一系列的开发和发布，scikit-learn 已经发展成学术界和专业人士广泛使用的机器学习工具之一。

本章中，我们将学习构建一系列广泛使用的建模算法，即线性回归和逻辑回归、支持向量机（SVM）、决策树和随机森林。首先，我们将介绍线性回归和逻辑回归。

线性回归与逻辑回归简介

在回归分析中，使用一个或多个自变量来预测单一的因变量或结果变量。回归的应用场景包括但不限于以下预测：

  • 根据各种球队统计数据预测球队的胜率

  • 根据家族病史及一系列身体和心理特征预测患心脏病的风险

  • 根据多个气候指标预测降雪的可能性

由于线性回归和逻辑回归具有易于解释和透明的特点，并且能够对未在训练数据中出现的值进行外推，因此它们是预测此类结果的流行选择。线性回归的最终目标是绘制一条直线，使得这条直线与观测值之间的绝对距离最小（即最佳拟合线）。因此，在线性回归中，假设特征与连续因变量之间的关系是线性的。线的形式通常是斜截式（即 y = a + bx），其中 a 为截距（即当 x 为 0 时 y 的值），b 为斜率，x 为自变量。本章将介绍两种线性回归：简单线性回归和多重线性回归。

简单线性回归

简单线性回归模型通过y = α + β**x定义一个特征与连续结果变量之间的关系。这个方程类似于斜截式，其中y表示因变量的预测值，α表示截距，β（贝塔）代表斜率，x是自变量的值。给定x值后，回归模型计算出能够最小化预测的y值（即ŷ）与实际y值之间绝对差异的α和β的值。

例如，如果我们使用身高（米）作为唯一预测变量来预测一个人的体重（千克），并且简单线性回归模型计算出α的值为 1.5，β的系数为 50，那么该模型可以解释为：每增加 1 米身高，体重大约增加 50 千克。因此，我们可以预测身高为 1.8 米的人的体重大约是 91.5 千克，计算公式为 y = 1.5 + (50 x 1.8)。在接下来的练习中，我们将演示如何使用 scikit-learn 进行简单线性回归。

练习 21：为线性回归模型准备数据

为了准备我们的数据以用于简单的线性回归模型，我们将使用一个随机子集，该子集来自 2006 至 2016 年间匈牙利塞格德市的天气数据集。该数据集包含从 2006 年 4 月 1 日到 2016 年 9 月 9 日的每小时天气测量数据。经过处理的数据以.csv文件形式提供（https://github.com/TrainingByPackt/Data-Science-with-Python/blob/master/Chapter02/weather.csv），并包含 10,000 条观察记录，涵盖 8 个变量：

  • Temperature_c：温度，单位为摄氏度

  • Humidity：湿度比例

  • Wind_Speed_kmh：风速，单位为公里每小时

  • Wind_Bearing_Degrees：风向，按顺时针方向从正北开始的角度

  • Visibility_km：能见度，单位为公里

  • Pressure_millibars：大气压力，单位为毫巴

  • Rain：雨=1，雪=0

  • Description：温暖、正常或寒冷

  1. 使用以下代码导入weather.csv数据集：

    import pandas as pd
df = pd.read_csv('weather.csv')

  2. 使用df.info()探索数据：https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_01.jpg

    ](https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_01.jpg)

    图 3.1：描述 df 的信息

  3. Description列是df中的唯一类别变量。可以按如下方式检查Description中的层级数量：

    levels = len(pd.value_counts(df['Description']))
print('There are {} levels in the Description column'.format(levels))

    层级的数量如下图所示：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_02.jpg

    图 3.2：'Description’列中的层级数量
    注意

    多类类别变量必须通过一种称为“虚拟编码”的过程转换为虚拟变量。对多类类别变量进行虚拟编码会创建 n-1 个新的二元特征，这些特征对应于类别变量中的层级。例如，一个具有三个层级的多类类别变量将创建两个二元特征。经过虚拟编码后，必须删除原始特征。

  4. 要对所有多分类的类别变量进行虚拟编码，请参考以下代码：

    import pandas as pd
df_dummies = pd.get_dummies(df, drop_first=True)
    注意

    原始的 DataFrame df包含八列，其中一列（即Description）是一个具有三个级别的多分类类别变量。

  5. 在第 4 步中，我们将这个特征转换为 n-1（即 2）个分开的虚拟变量，并删除了原始特征Description。因此，df_dummies现在应该包含比df多一列（即 9 列）。使用以下代码检查这一点：

    print('There are {} columns in df_dummies'	.format(df_dummies.shape[1]))

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_03.jpg

    图 3.3：虚拟编码后列的数量

  6. 为了消除数据中可能存在的顺序效应，良好的实践是先对数据的行进行洗牌，然后再将数据拆分为特征（X）和结果（y）。要对df_dummies中的行进行洗牌，请参考以下代码：

    from sklearn.utils import shuffle
df_shuffled = shuffle(df_dummies, random_state=42)

  7. 现在数据已经被洗牌，我们将把数据的行拆分为特征（X）和因变量（y）。

    注意

    线性回归用于预测连续的结果。因此，在本次练习中，我们假设连续变量Temperature_c（摄氏温度）是因变量，我们正在准备数据来拟合一个线性回归模型。

  8. 将df_shuffled拆分为X和y如下所示：

    DV = 'Temperature_c'
X = df_shuffled.drop(DV, axis=1)
y = df_shuffled[DV]

  9. 使用以下代码将X和y拆分为测试数据和训练数据：

    from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

    现在，数据已经进行了虚拟编码、洗牌、拆分成X和y，并进一步划分为测试数据集和训练数据集，准备好用于线性回归或逻辑回归模型。

    这里的截图展示了X_train的前五行：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_04.jpg

图 3.4：X_train的前五行

练习 22：拟合简单线性回归模型并确定截距和系数

在本次练习中，我们将继续使用练习 21 中准备的数据，通过简单线性回归模型来预测摄氏温度与湿度之间的关系。

从练习 21 继续，执行以下步骤：

  1. 要实例化一个线性回归模型，请参考以下代码：

    from sklearn.linear_model import LinearRegression
model = LinearRegression()

  2. 使用以下代码将模型拟合到训练数据中的Humidity列：

    model.fit(X_train[['Humidity']], y_train)

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_05.jpg

    图 3.5：拟合简单线性回归模型的输出

  3. 使用以下代码提取截距的值：

    intercept = model.intercept_

  4. 使用以下代码提取coefficient的值：

    coefficient = model.coef_

  5. 现在，我们可以使用以下代码打印出预测摄氏温度的公式：

    print('Temperature = {0:0.2f} + ({1:0.2f} x Humidity)'.format(intercept, coefficient[0]))

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_06.jpg

图 3.6：使用简单线性回归从湿度预测摄氏温度的公式

干得好！根据这个简单线性回归模型，一个湿度值为 0.78 的日子预测温度为 10.56 摄氏度。现在我们已经熟悉了提取简单线性回归模型的截距和系数，是时候生成预测并评估模型在未见过的测试数据上的表现了。

教学提示

练习在不同湿度水平下计算温度。

练习 23：生成预测并评估简单线性回归模型的表现

监督学习的核心目的是使用现有的标记数据生成预测。因此，本练习将演示如何在测试特征上生成预测，并通过将预测与实际值进行比较来生成模型性能指标。

从练习 22继续，执行以下步骤：

  1. 使用以下代码在测试数据上生成预测：

    predictions = model.predict(X_test[['Humidity']])
    注意

    评估模型性能的一种常见方法是使用散点图检查预测值与实际值之间的相关性。散点图展示了实际值与预测值之间的关系。一个完美的回归模型将在预测值和实际值之间显示一条直线。预测值与实际值之间的关系可以通过皮尔逊 r 相关系数来量化。在接下来的步骤中，我们将创建一个预测值与实际值的散点图。

  2. 如果相关系数显示在图表标题中会更有帮助。以下代码将演示如何做到这一点：

    import matplotlib.pyplot as plt
from scipy.stats import pearsonr
plt.scatter(y_test, predictions)
plt.xlabel('Y Test (True Values)')
plt.ylabel('Predicted Values')
plt.title('Predicted vs. Actual Values (r = {0:0.2f})'.format(pearsonr(y_test, predictions)[0], 2))
plt.show()

    这是生成的输出结果：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_07.jpg

    图 3.7：简单线性回归模型的预测值与实际值对比
    注意

    皮尔逊 r 值为 0.62，表明预测值与实际值之间存在中等程度的正向线性相关性。一个完美的模型会使散点图中的所有点都在一条直线上，并且 r 值为 1.0。

  3. 一个与数据拟合得非常好的模型，其残差应该呈正态分布。要创建残差的密度图，请参照以下代码：

    import seaborn as sns
from scipy.stats import shapiro
sns.distplot((y_test - predictions), bins = 50)
plt.xlabel('Residuals')
plt.ylabel('Density')
plt.title('Histogram of Residuals (Shapiro W p-value = {0:0.3f})'.format(shapiro(y_test - predictions)[1]))
plt.show()

    请参阅此处的输出结果：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_08.jpg

    图 3.8：简单线性回归模型的残差直方图
    注意

    直方图显示残差呈负偏态，标题中的 Shapiro W p 值告诉我们该分布不是正态分布。这进一步证明我们的模型还有改进空间。

  4. 最后，我们将计算平均绝对误差、均方误差、均方根误差和 R 平方值，并使用以下代码将它们放入一个数据框中：

    from sklearn import metrics
import numpy as np
metrics_df = pd.DataFrame({'Metric': ['MAE', 
                                      'MSE', 
                                      'RMSE', 
                                      'R-Squared'],
                          'Value': [metrics.mean_absolute_error(y_test, predictions),
                                    metrics.mean_squared_error(y_test, predictions),
                                    np.sqrt(metrics.mean_squared_error(y_test, predictions)),
                                    metrics.explained_variance_score(y_test, predictions)]}).round(3)
print(metrics_df)

    请参阅生成的输出结果：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_09.jpg

图 3.9：简单线性回归模型的模型评估指标

平均绝对误差（MAE）是预测值与实际值之间的平均绝对差。均方误差（MSE）是预测值与实际值之间差的平方的平均值。均方根误差（RMSE）是 MSE 的平方根。R 方告诉我们可以由模型解释的因变量方差的比例。因此，在这个简单线性回归模型中，湿度仅能解释温度方差的 38.9%。此外，我们的预测值在±6.052 摄氏度范围内。

在这里，我们成功地使用 scikit-learn 拟合和评估了一个简单线性回归模型。这是成为机器学习专家之旅中的第一步。接下来，我们将继续扩展我们对回归的知识，并通过探索多元线性回归来改进这个模型。

多元线性回归

多元线性回归模型通过 y = α + β1x**i1 + β2x**i2 + … + βp-1x**i,p-1 定义了两个或更多特征与连续结果变量之间的关系。再次说明，α 表示截距，β 表示模型中每个特征（x）的斜率。因此，如果我们使用身高（m）、总胆固醇（mg/dL）和每日心血管运动分钟数来预测个体的体重（kg），且多元线性回归模型计算出 α 为 1.5，β**1 为 50，β**2 为 0.1，β**3 为-0.4，这个模型可以解释为：在控制模型中的所有其他特征的情况下，每增加 1 m 的身高，体重增加 50 kg。此外，每增加 1 mg/dL 的总胆固醇，体重增加 0.1 kg。最后，每天每增加 1 分钟的心血管运动，体重减少 0.4 kg。因此，我们可以预测一个身高为 1.8 m、总胆固醇为 200 mg/dL，并每天完成 30 分钟心血管运动的个体的体重为 99.5 kg，使用 y = 1.5 + (0.1 x 50) + (200 x 0.5) + (30 x -0.4)。在下一项练习中，我们将演示如何使用 scikit-learn 进行多元线性回归。

练习 24：拟合多元线性回归模型并确定截距和系数

在这个练习中，我们将继续使用我们在练习 21中准备的数据，拟合一个多元线性回归模型，以预测数据中所有特征对应的温度（摄氏度）。

继续自练习 23，执行以下步骤：

  1. 要实例化一个线性回归模型，请参考以下代码：

    from sklearn.linear_model import LinearRegression
model = LinearRegression()

  2. 使用以下代码将模型拟合到训练数据中：

    model.fit(X_train, y_train)

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_10.jpg

    图 3.10：拟合多元线性回归模型的输出结果

  3. 使用以下代码提取截距值：

    intercept = model.intercept_

  4. 按照以下方法提取系数值：

    coefficients = model.coef_

  5. 现在，我们可以打印出一个消息，显示使用此代码预测摄氏温度的公式：

    print('Temperature = {0:0.2f} + ({1:0.2f} x Humidity) + ({2:0.2f} x Wind Speed) + ({3:0.2f} x Wind Bearing Degrees) + ({4:0.2f} x Visibility) + ({5:0.2f} x Pressure) + ({6:0.2f} x Rain) + ({7:0.2f} x Normal Weather) + ({8:0.2f} x Warm Weather)'.format(intercept,
coefficients[0],
coefficients[1],
coefficients[2],
coefficients[3],
coefficients[4],
coefficients[5],
coefficients[6],
coefficients[7]))

    我们的输出应如下所示：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_11.jpg

图 3.11：使用多元线性回归根据湿度预测摄氏温度的公式

做得好！根据这个多元回归模型，一天湿度为 0.78，风速为 5.0 km/h，风向为自正北顺时针 81 度，能见度为 3 km，气压为 1000 毫巴，没有降雨，且天气被描述为正常，那么该天预测的摄氏温度为 5.72 度。现在我们已经熟悉了如何提取多元线性回归模型的截距和系数，我们可以生成预测并评估模型在测试数据上的表现。

活动 5：生成预测并评估多元线性回归模型的性能

在练习 23中，生成预测并评估简单线性回归模型的性能，我们学习了如何使用多种方法生成预测并评估简单线性回归模型的性能。为了减少代码的冗余，我们将使用练习 23中步骤 4的指标来评估多元线性回归模型的性能，并确定多元线性回归模型相对于简单线性回归模型的表现是更好还是更差。

从练习 24 开始，执行以下步骤：

  1. 使用所有特征在测试数据上生成预测。

  2. 使用散点图绘制预测值与实际值的关系。

  3. 绘制残差的分布图。

  4. 计算均值绝对误差、均方误差、均方根误差和 R 平方，并将结果放入 DataFrame 中。

  5. 确定多元线性回归模型相较于简单线性回归模型的表现是更好还是更差。

    注意

    此活动的解决方案可以在第 343 页找到。

你应该发现，相较于简单线性回归模型，多元线性回归模型在每个指标上表现得更好。最显著的是，在简单线性回归模型中，模型只能解释温度方差的 38.9%。然而，在多元线性回归模型中，特征的组合解释了 86.6% 的温度方差。此外，我们的简单线性回归模型预测的温度平均误差为 ± 6.052 度，而我们的多元线性回归模型预测的温度平均误差为 ± 2.861 度。

截距和回归系数的透明性使得线性回归模型非常易于解释。在商业中，通常要求数据科学家解释某一特征对结果的影响。因此，线性回归提供了可用的指标，从而合理回应了之前的业务询问。

然而，大多数情况下，问题要求数据科学家预测一个不是连续的，而是分类的结果变量。例如，在保险领域，给定客户的某些特征，预测该客户是否会续保的概率是多少？在这种情况下，数据中的特征与结果变量之间不存在线性关系，因此线性回归方法会失败。对于分类因变量，进行回归分析的一个可行选择是逻辑回归。

逻辑回归

逻辑回归使用分类变量和连续变量来预测分类结果。当所选因变量有两个分类结果时，分析称为二元逻辑回归。然而，如果结果变量有多个水平，则该分析称为多项式逻辑回归。本章的学习将集中在前者上。

在预测二元结果时，特征与结果变量之间并不存在线性关系，这违反了线性回归的假设。因此，为了以线性方式表达非线性关系，我们必须使用对数转换来转换数据。因此，逻辑回归使我们能够预测在给定模型中特征的情况下二元结果发生的概率。

对于具有 1 个预测变量的逻辑回归，逻辑回归方程如下所示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_12.jpg

图 3.12：具有 1 个预测变量的逻辑回归公式

在上图中，P(Y) 是结果发生的概率，e 是自然对数的底数，α 是截距，β 是回归系数，x 是预测变量的值。该方程可以扩展到多个预测变量，使用以下公式：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_13.jpg

图 3.13：具有多个预测变量的逻辑回归公式

因此，使用逻辑回归来建模事件发生的概率，就相当于拟合一个线性回归模型，只是连续的结果变量已被替换为成功的对数比（另一种表达概率的方式），用于二元结果变量。在线性回归中，我们假设预测变量与结果变量之间存在线性关系。而逻辑回归则假设预测变量与 p/(1-p) 的自然对数之间存在线性关系，其中 p 是事件发生的概率。

在接下来的练习中，我们将使用 weather.csv 数据集，演示如何构建一个逻辑回归模型，利用我们数据中的所有特征来预测降雨的概率。

练习 25：拟合逻辑回归模型并确定截距和系数

为了使用数据中的所有特征来建模降雨的概率（而非雪），我们将使用 weather.csv 文件，并将二元变量 Rain 作为结果测量。

  1. 使用以下代码导入数据：

    import pandas as pd
df = pd.read_csv('weather.csv')

  2. 如下所示对 Description 变量进行虚拟编码：

    import pandas as pd
df_dummies = pd.get_dummies(df, drop_first=True)

  3. 使用此处的代码对 df_dummies 进行洗牌：

    from sklearn.utils import shuffle
df_shuffled = shuffle(df_dummies, random_state=42)

  4. 如下所示，将特征和结果分别拆分为 X 和 y：

    DV = 'Rain' 
X = df_shuffled.drop(DV, axis=1) 
y = df_shuffled[DV]

  5. 使用以下代码将特征和结果拆分为训练数据和测试数据：

    from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

  6. 使用以下代码实例化一个逻辑回归模型：

    from sklearn.linear_model import LogisticRegression
model = LogisticRegression()

  7. 使用 model.fit(X_train, y_train) 将逻辑回归模型拟合到训练数据中。我们应该得到以下输出：https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_14.jpg

    图 3.14：拟合逻辑回归模型的输出

  8. 使用以下代码获取截距：

    intercept = model.intercept_

  9. 使用以下代码提取系数：

    coefficients = model.coef_

  10. 如下所示，将系数放入列表：

    coef_list = list(coefficients[0,:])

  11. 将特征与它们的系数匹配，放入 DataFrame 中，并按如下方式将 DataFrame 打印到控制台：

    coef_df = pd.DataFrame({'Feature': list(X_train.columns),
                        'Coefficient': coef_list})
print(coef_df)

    请参考此处的输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_15.jpg

图 3.15：逻辑回归模型的特征及其系数

温度的系数可以解释为：每增加 1 度温度，降雨的对数几率增加 5.69，同时控制模型中的其他特征。为了生成预测，我们可以将对数几率转换为几率，再将几率转换为概率。然而，scikit-learn 提供了生成预测概率以及预测类别的功能。

练习 26：生成预测并评估逻辑回归模型的表现

在练习 25中，我们学习了如何拟合一个逻辑回归模型，并提取生成预测所需的元素。然而，scikit-learn 通过提供函数来预测结果的概率以及预测结果的类别，使我们的工作变得更加轻松。在本练习中，我们将学习如何生成预测的概率和类别，并使用混淆矩阵和分类报告评估模型的表现。

从练习 25 开始，执行以下步骤：

  1. 使用以下代码生成预测概率：

    predicted_prob = model.predict_proba(X_test)[:,1]

  2. 使用以下代码生成预测类别：

    predicted_class = model.predict(X_test)

  3. 使用混淆矩阵按如下方式评估表现：

    from sklearn.metrics import confusion_matrix
import numpy as np
cm = pd.DataFrame(confusion_matrix(y_test, predicted_class))
cm['Total'] = np.sum(cm, axis=1)
cm = cm.append(np.sum(cm, axis=0), ignore_index=True)
cm.columns = ['Predicted No', 'Predicted Yes', 'Total']
cm = cm.set_index([['Actual No', 'Actual Yes', 'Total']])
print(cm)

    请参考此处的输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_16.jpg

    图 3.16：我们逻辑回归模型的混淆矩阵
    注意

    从混淆矩阵中，我们可以看到，在 383 个未被分类为“雨天”的观测值中，377 个被正确分类；在 2917 个被分类为“雨天”的观测值中，2907 个被正确分类。为了进一步检查我们模型的性能，我们将使用精度、召回率和f1得分等指标生成分类报告。

  4. 使用以下代码生成分类报告：

    from sklearn.metrics import classification_report
print(classification_report(y_test, predicted_class))

    请参考结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_17.jpg

图 3.17：我们逻辑回归模型生成的分类报告

从我们的混淆矩阵和分类报告中可以看出，我们的模型表现非常好，可能很难进一步改进。然而，机器学习模型，包括逻辑回归，包含许多可以调整的超参数，调优这些超参数可以进一步提高模型性能。在下一个练习中，我们将学习如何找到超参数的最佳组合，以最大化模型性能。

练习 27：调优多重逻辑回归模型的超参数

在练习 25的步骤 7中，我们拟合了一个逻辑回归模型，随后该模型的输出显示在图 3.14 中。LogisticRegression()函数中的每个参数都设置为默认超参数。为了调优模型，我们将使用 scikit-learn 的网格搜索功能，它会为每个可能的超参数值组合拟合模型，并确定每个超参数的最佳值，从而得到最好的模型。在本练习中，我们将学习如何使用网格搜索来调优模型。

继续从练习 26：

  1. 数据已经为我们准备好了（见练习 26）；因此，我们可以直接开始实例化一个可能的超参数值网格，如下所示：

    import numpy as np
grid = {'penalty': ['l1', 'l2'],
        'C': np.linspace(1, 10, 10),
        'solver': ['liblinear']}

  2. 实例化一个网格搜索模型，寻找具有最大f1得分（即精度和召回率的调和平均数）的模型，如下所示：

    from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
model = GridSearchCV(LogisticRegression(solver='liblinear'), grid, scoring='f1', cv=5)

  3. 使用model.fit(X_train, y_train)在训练集上拟合模型（请记住，这可能需要一些时间），并找到此处的结果输出：https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_18.jpg

    图 3.18：我们逻辑回归网格搜索模型的输出

  4. 我们可以如下所示返回超参数的最佳组合，以字典形式表示：

    best_parameters = model.best_params_
print(best_parameters)

    请参考此处的结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_19.jpg

图 3.19：我们逻辑回归网格搜索模型调优后的超参数

我们已经找到了最大化f1得分的超参数组合。请记住，仅仅使用练习 25中的默认超参数就能得到一个在测试数据上表现非常好的模型。因此，在接下来的活动中，我们将评估调优过的超参数模型在测试数据上的表现。

活动 6：生成预测并评估调优后的逻辑回归模型性能

一旦找到了最佳的超参数组合，我们需要像在练习 25 中一样评估模型的性能。

从练习 27 继续：

  1. 生成预测的降雨概率。

  2. 生成预测的降雨类别。

  3. 使用混淆矩阵评估性能，并将其存储为数据框。

  4. 打印分类报告。

    注意

    此活动的解决方案可以在第 346 页找到。

通过调整逻辑回归模型的超参数，我们能够改进已经表现非常良好的逻辑回归模型。我们将在接下来的练习和活动中继续扩展调整不同类型的模型。

最大边界分类使用 SVM

SVM 是一种监督学习算法，可以解决分类和回归问题。然而，SVM 最常用于分类问题，因此，在本章中，我们将重点讨论 SVM 作为二分类器。SVM 的目标是确定超平面的最佳位置，在多维空间中创建数据点之间的类别边界。为帮助澄清这一概念，请参见图 3.20。

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_20.jpg

图 3.20：超平面（蓝色）在三维空间中将圆形与方形分开

在图 3.20 中，方形和圆形是同一数据框中的观测值，代表不同的类别。在该图中，超平面由一个半透明的蓝色边界表示，位于圆形和方形之间，划分出两个不同的类别。在这个例子中，观测点被认为是线性可分的。

超平面的位置是通过找到在两类之间创建最大分隔（即边界）的位置来确定的。因此，这被称为最大边界超平面（MMH），并提高了点保持在超平面边界正确一侧的可能性。可以通过每个类中最接近 MMH 的点来表达 MMH。这些点被称为支持向量，每个类至少有 1 个。图 3.21 直观地展示了支持向量与 MMH 在二维空间中的关系：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_21.jpg

图 3.21：支持向量与 MMH 的关系

实际上，大多数数据是不可线性分割的。在这种情况下，SVM 使用松弛变量，创建一个软边界（与最大边界相对），允许一些观测点落在边界的错误一侧。请参见以下图示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_22.jpg

图 3.22：两个观测值（用灰色阴影和希腊字母Χi 表示）位于软边界线的错误一侧

对误分类的数据点应用一个成本值，算法的目标不是找到最大边界，而是最小化总成本。随着成本参数的增加，SVM 优化将更加严格，目标是 100%的分类分离，这可能导致过拟合训练数据。相反，较低的成本参数则强调更宽的边界，可能导致欠拟合训练数据。因此，为了创建在测试数据上表现良好的 SVM 模型，重要的是确定一个平衡过拟合和欠拟合的成本参数。

此外，非线性可分的数据可以通过使用核技巧转换到更高维度的空间。在映射到高维空间后，原本的非线性关系可能变得线性。通过对原始数据进行转换，SVM 可以发现原始特征中没有明确体现的关联。scikit-learn 默认使用高斯 RBF 核，但也提供了常用的核函数，如线性核、多项式核和 sigmoid 核。为了最大化 SVM 分类器模型的性能，必须确定核函数和成本函数的最佳组合。幸运的是，可以通过网格搜索超参数调整轻松实现这一点，正如练习 27 中介绍的那样。在接下来的练习和活动中，我们将学习如何实现这一目标。

练习 28：为支持向量分类器（SVC）模型准备数据

在为预测二元结果变量（在此案例中为雨或雪）拟合 SVM 分类器模型之前，我们必须先准备数据。由于 SVM 是一个“黑箱”模型，即输入和输出之间的过程不明确，因此我们不需要担心模型的可解释性。因此，在拟合模型之前，我们将数据中的特征转换为 z 分数。以下步骤将展示如何进行：

  1. 使用以下代码导入weather.csv：

    import pandas as pd
df = pd.read_csv('weather.csv')

  2. 将分类特征Description进行虚拟编码，方法如下：

    import pandas as pd
df_dummies = pd.get_dummies(df, drop_first=True)

  3. 使用以下代码对df_dummies进行洗牌，以去除任何排序效应：

    from sklearn.utils import shuffle
df_shuffled = shuffle(df_dummies, random_state=42)

  4. 使用以下代码将df_shuffled拆分为X和y：

    DV = 'Rain'
X = df_shuffled.drop(DV, axis=1) 
y = df_shuffled[DV]

  5. 使用以下代码将X和y划分为测试数据和训练数据：

    from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

  6. 为了防止数据泄漏，通过拟合一个缩放器模型到X_train并分别将其转换为 z 分数，按如下方式对X_train和X_test进行缩放：

    from sklearn.preprocessing import StandardScaler
model = StandardScaler() 
X_train_scaled = model.fit_transform(X_train)
X_test_scaled = model.transform(X_test)

现在，我们的数据已经正确地划分为特征和结果变量，分为测试数据和训练数据，并且已分别进行了缩放，因此我们可以使用网格搜索调整 SVC 模型的超参数。

练习 29：使用网格搜索调整 SVC 模型

之前，我们讨论了确定 SVM 分类器模型的最佳成本函数和核函数的重要性。在练习 27 中，我们学习了如何使用 scikit-learn 的网格搜索功能找到超参数的最佳组合。在本练习中，我们将演示如何使用网格搜索来找到最佳的成本函数和核函数组合。

从练习 28继续：

  1. 使用以下代码实例化要搜索的网格：

    import numpy as np
grid = {'C': np.linspace(1, 10, 10),
        'kernel': ['linear', 'poly', 'rbf', 'sigmoid']}

  2. 使用 gamma 超参数设置为 auto 来避免警告，并将概率设置为 True，以便我们可以提取雨的概率，如下所示：

    from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
model = GridSearchCV(SVC(gamma='auto'), grid, scoring='f1', cv=5)

  3. 使用 model.fit(X_train_scaled, y_train) 拟合网格搜索模型：https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_23.jpg

    图 3.23：拟合 SVC 网格搜索模型的输出

  4. 使用以下代码打印最佳参数：

    best_parameters = model.best_params_
print(best_parameters)

    参见下面的结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_24.jpg

图 3.24：我们 SVC 网格搜索模型的调优超参数

一旦确定了超参数的最佳组合，就可以开始生成预测，并随后评估我们的模型在未见测试数据上的表现。

活动 7：生成预测并评估 SVC 网格搜索模型的性能

在之前的练习/活动中，我们学习了如何生成预测并评估分类器模型的性能。在本活动中，我们将再次评估模型的性能，通过生成预测、创建混淆矩阵并打印分类报告。

从练习 29 继续：

  1. 提取预测的类别。

  2. 创建并打印混淆矩阵。

  3. 生成并打印分类报告。

    注意

    本活动的解决方案可以在第 348 页找到。

在这里，我们展示了如何通过网格搜索调优 SVC 模型的超参数。调优后的 SVC 模型在预测雨/雪方面的表现不如调优后的逻辑回归模型。此外，SVC 模型是一个黑箱，因为它们无法提供特征对结果的贡献的洞察。在接下来的决策树部分，我们将介绍一种不同的算法——决策树，它采用“分而治之”的方法生成预测，并提供特征重要性属性，用于确定每个特征对结果的影响。

决策树

假设我们正在考虑换工作。我们正在权衡潜在工作机会的利弊，在当前职位待了几年后，我们开始意识到对我们来说重要的东西。然而，职业的各个方面并非都同等重要。事实上，在工作几年后，我们决定职位最重要的方面是我们对所做项目的兴趣，其次是薪酬，再然后是工作压力，接着是通勤时间，最后是福利。我们刚刚创建了一个认知决策树的框架。我们可以进一步详细说明，我们希望找到一份工作，其中分配的项目我们非常感兴趣，年薪至少为$55k，工作压力较低，通勤时间不超过 30 分钟，并且有良好的牙科保险。创建心理决策树是我们天生就会利用的一种决策过程，也是决策树成为当今最广泛使用的机器学习算法之一的原因。

在机器学习中，决策树使用基尼不纯度或熵信息增益作为衡量拆分质量的标准。首先，决策树算法确定能够最大化拆分质量值的特征。这被称为根节点，因为它是数据中最重要的特征。在前面提到的工作机会中，对潜在项目非常感兴趣会被视为根节点。考虑到根节点，工作机会被分为那些有非常有趣项目的和那些没有非常有趣项目的。

接下来，在考虑前一个特征的基础上，将这两个类别细分为下一个最重要的特征，以此类推，直到潜在工作被识别为感兴趣或不感兴趣。

这种方法被称为递归划分，或称为"分而治之"，因为它持续不断地拆分和细分数据，直到算法判断数据子集已足够同质化，或者：

  • 对应节点的几乎所有观察结果都属于同一类别（即纯度）。

  • 数据中没有进一步的特征可供拆分。

  • 树已达到事先决定的大小限制。

例如，如果纯度是通过熵来决定的，我们必须理解熵是衡量一组值内部随机性的指标。决策树通过选择最小化熵（随机性）的切分来运作，进而最大化信息增益。信息增益是通过计算切分与所有后续切分之间的熵差值来确定的。然后，计算总熵的方法是将每个分区的熵加权求和，权重是该分区中观察值的比例。幸运的是，scikit-learn 提供了一个函数来帮助我们完成这些操作。在接下来的练习和活动中，我们将实现决策树分类器模型，用以预测是否在下雨或下雪，使用熟悉的weather.csv数据集。

活动 8：为决策树分类器准备数据

在本活动中，我们将为决策树分类器模型准备数据。执行以下步骤完成活动：

  1. 导入weather.csv并将其存储为 DataFrame

  2. 为多层次的分类特征Summary编写虚拟代码

  3. 打乱数据，以去除可能的顺序效应

  4. 将数据拆分为特征和结果

  5. 进一步将特征和结果拆分为测试数据和训练数据

  6. 使用以下代码缩放X_train和X_test：

    from sklearn.preprocessing import StandardScaler
model = StandardScaler()
X_train_scaled = model.fit_transform(X_train)
X_test_scaled = model.transform(X_test)
    注意

    本活动的解决方案可以在第 349 页找到

在接下来的练习中，我们将学习如何调优和拟合决策树分类器模型。

练习 30：使用网格搜索调优决策树分类器

在本练习中，我们将实例化一个超参数空间，并使用网格搜索来调优决策树分类器的超参数。

继续进行活动 8，执行以下步骤：

  1. 按如下方式指定超参数空间：

    import numpy as np
grid = {'criterion': ['gini', 'entropy'],
        'min_weight_fraction_leaf': np.linspace(0.0, 0.5, 10),
        'min_impurity_decrease': np.linspace(0.0, 1.0, 10),
        'class_weight': [None, 'balanced'],
'presort': [True, False]}Instantiate the GridSearchCV model

  2. 使用以下代码实例化网格搜索模型：

    from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
model = GridSearchCV(DecisionTreeClassifier(), grid, scoring='f1', cv=5)

  3. 使用以下方法拟合训练集：

    model.fit(X_train_scaled, y_train)

    查看此处显示的结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_25.jpg

    图 3.25：拟合我们的决策树分类器网格搜索模型的输出

  4. 打印调优后的参数：

    best_parameters = model.best_params_
print(best_parameters)

    查看下面的结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_26.jpg

图 3.26：我们决策树分类器网格搜索模型的调优超参数

我们可以从图 3.26 中看到，它使用了gini不纯度作为切分质量的标准。关于超参数的进一步解释超出了本章范围，但可以在决策树分类器的 scikit-learn 文档中找到。

记住，在实际应用中，决策者常常会询问不同特征如何影响预测。在线性回归和逻辑回归中，截距和系数使得模型预测非常透明。

注意

决策树也非常容易解释，因为我们可以看到做出决策的地方，但这需要安装并正确配置 Graphviz，并且特征需要未经过缩放。

与接下来的练习不同，我们将探索 scikit-learn 树形模型算法中找到的一个属性 ‘feature_importances_’，该属性返回一个包含每个特征相对重要性值的数组。需要注意的是，这个属性在网格搜索模型中不可用。因此，在下一个练习中，我们将学习如何从 best_parameters 字典中程序化提取值，并重新拟合调优后的决策树模型，从而访问决策树分类器函数提供的属性。

练习 31：程序化地从决策树分类器网格搜索模型中提取调优后的超参数

在前一个练习中，我们将调优后的超参数保存为 best_parameters 字典中的键值对。这使我们能够以编程方式访问这些值并将它们分配给决策树分类器模型的相应超参数。通过拟合调优后的决策树模型，我们将能够访问 scikit-learn 决策树分类器函数提供的属性。

继续进行 练习 30，执行以下步骤：

  1. 证明我们可以通过以下方式访问 ‘Tree_criterion’ 的值：

    print(best_parameters['criterion'])

    在这里查看结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_27.jpg

    图 3.27：在 best_parameters 字典中分配给 ‘Tree_criterion’ 键的值

  2. 实例化决策树分类器模型，并将相应的超参数值分配如下：

    from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(class_weight=best_parameters['class_weight'],
                               criterion=best_parameters['criterion'],
                      min_impurity_decrease=best_parameters['min_impurity_decrease'],
               min_weight_fraction_leaf=best_parameters['min_weight_fraction_leaf'],
                               presort=best_parameters['presort'])

  3. 使用以下代码将网格搜索模型拟合到标准化的训练数据：

    model.fit(X_train_scaled, y_train)

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_28.jpg

    图 3.28：使用调优后的超参数拟合决策树分类器模型的输出

  4. 使用以下代码提取 feature_importances 属性：

    print(model.feature_importances_)
The resultant output is shown below:

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_29.jpg

    图 3.29：我们调优后的决策树分类器模型的特征重要性数组

    从图 3.29 的数组中，我们可以看到第一个特征在特征重要性上完全主导了其他变量。

  5. 使用以下代码可视化：

    import pandas as pd
import matplotlib.pyplot as plt
df_imp = pd.DataFrame({'Importance': list(model.feature_importances_)}, index=X.columns)
df_imp_sorted = df_imp.sort_values(by=('Importance'), ascending=True)
df_imp_sorted.plot.barh(figsize=(5,5))
plt.title('Relative Feature Importance')
plt.xlabel('Relative Importance')
plt.ylabel('Variable')
plt.legend(loc=4)
plt.show()

    在这里查看结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_30.jpg

图 3.30：调优后的决策树分类器模型的特征重要性

看起来摄氏温度是这个分类问题的唯一驱动因素。由于结果衡量标准是 rain ('Rain'=1) 或 snow ('Rain'=0)，而决策树通过“分而治之”的方式做出划分决策，因此算法使用温度来判断测量时是否有降雨或降雪，这也有其合理性。在接下来的活动中，我们将评估模型的表现。

活动 9：生成预测并评估决策树分类器模型的性能

在之前的练习和活动中，我们已经生成了预测并评估了模型性能。在本次活动中，我们将采取相同的方法来评估我们调整过的决策树分类器模型的性能。

从第 31 次练习继续，执行以下步骤：

  1. 生成降水的预测概率。

  2. 生成降水的预测类别。

  3. 生成并打印混淆矩阵。

  4. 打印分类报告。

    注意

    本活动的解决方案可以在第 350 页找到。

你应该会发现只有一个观测值被误分类。因此，通过在我们的 weather.csv 数据集上调整决策树分类器模型，我们能够高精度地预测降雨（或降雪）。我们可以看到，唯一的驱动特征是摄氏温度。这是有道理的，因为决策树使用递归分割的方法来进行预测。

有时候，经过评估后，单一模型是一个弱学习器，表现不佳。然而，通过组合多个弱学习器，我们可以创建一个更强的学习器。将多个弱学习器组合成一个强学习器的方式称为集成。随机森林模型将多个决策树模型组合在一起，形成一个更强的集成模型。随机森林可以用于分类或回归问题。

随机森林

如前所述，随机森林是决策树的集成，可以用来解决分类或回归问题。随机森林使用数据的一小部分来拟合每棵树，因此能够处理非常大的数据集，而且相较于其他算法，它们对“维度灾难”的敏感性较低。维度灾难是指数据中有大量特征时，模型的性能会下降。随机森林的预测是通过将每棵树的预测结果结合起来得到的。与支持向量机（SVM）一样，随机森林是一个黑箱，其输入和输出无法解释。

在接下来的练习和活动中，我们将使用网格搜索调整并拟合随机森林回归器，以预测摄氏温度。然后，我们将评估模型的性能。

练习 32：为随机森林回归器准备数据

首先，我们将为随机森林回归器准备数据，使用 ‘Temperature_c’ 作为因变量，就像我们在第 21 次练习中做的那样：

  1. 导入 ‘weather.csv’ 并使用以下代码将其保存为 df：

    import pandas as pd
df = pd.read_csv('weather.csv')

  2. 对多类分类变量 Description 进行虚拟编码，方法如下：

    import pandas as pd
df_dummies = pd.get_dummies(df, drop_first=True)

  3. 使用以下代码通过打乱 df_dummies 来去除可能的排序效应：

    from sklearn.utils import shuffle
df_shuffled = shuffle(df_dummies, random_state=42)

  4. 使用以下代码将 df_shuffled 划分为 X 和 y：

    DV = 'Temperature_c'
X = df_shuffled.drop(DV, axis=1)
y = df_shuffled[DV]

  5. 将 X 和 y 按照如下方式划分为测试数据和训练数据：

    from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

  6. 使用以下代码对 X_train 和 X_test 进行缩放：

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

现在，我们已经导入、打乱、将数据分为特征（X）和因变量（y），将X和y拆分为测试数据和训练数据，并对X_train和X_test进行缩放，我们将使用网格搜索调优随机森林回归模型。

活动 10：调优随机森林回归模型

数据已准备好用于随机森林回归模型。现在，我们必须设置超参数空间，并使用网格搜索找到超参数的最佳组合。

从练习 32 继续，执行以下步骤：

  1. 指定超参数空间。

  2. 实例化GridSearchCV模型以优化解释方差。

  3. 将网格搜索模型拟合到训练集。

  4. 打印调优后的参数。

    注意

    该活动的解决方案可以在第 351 页找到。

在对我们的随机森林回归超参数进行网格搜索后，我们需要使用调优后的超参数拟合一个随机森林回归模型。我们将编程提取best_parameters字典中的值，并将它们分配给随机森林回归函数中的相应超参数，以便我们可以访问来自该函数的属性。

练习 33：从随机森林回归网格搜索模型中编程提取调优的超参数并确定特征重要性

通过从best_parameters字典中的键值对提取值，我们消除了手动错误的可能性，并且使我们的代码更加自动化。在本练习中，我们将复制练习 31中的步骤，但将代码调整为适应随机森林回归模型。

从活动 10继续，执行以下步骤：

  1. 实例化一个随机森林回归模型，将best_parameters字典中每个键的值分配给相应的超参数：

    from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(criterion=best_parameters['criterion'],
                              max_features=best_parameters['max_features'],
                              min_impurity_decrease=best_parameters['min_impurity_decrease'],
                              bootstrap=best_parameters['bootstrap'],
                              warm_start=best_parameters['warm_start'])

  2. 使用以下代码在训练数据上拟合模型：

    model.fit(X_train_scaled, y_train)

    在此处查找结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_31.jpg

    图 3.31：使用调优超参数拟合随机森林回归模型的输出

  3. 使用以下代码按降序绘制特征重要性：

    import pandas as pd
import matplotlib.pyplot as plt
df_imp = pd.DataFrame({'Importance': list(model.feature_importances_)}, index=X.columns)
df_imp_sorted = df_imp.sort_values(by=('Importance'), ascending=True)
df_imp_sorted.plot.barh(figsize=(5,5))
plt.title('Relative Feature Importance')
plt.xlabel('Relative Importance')
plt.ylabel('Variable')
plt.legend(loc=4)
plt.show()

    在此处查看结果输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_03_32.jpg

图 3.32：来自调优超参数的随机森林回归模型的特征重要性

从图 3.32 中，我们可以看到’Description_Warm’虚拟变量和’Humidity’是摄氏温度的主要驱动因素。与此同时，'Visibility_km’和’Wind_Bearing_degrees’对温度的影响较小。接下来，我们将检查我们的模型在测试数据上的表现。

活动 11：生成预测并评估调优后的随机森林回归模型的性能

在练习 23和活动 5中，我们学习了如何生成预测并评估回归模型在预测连续结果时的性能。在本次活动中，我们将采用相同的方法来评估我们随机森林回归模型在预测摄氏温度时的性能。

继续执行练习 33中的步骤，进行以下操作：

  1. 在测试数据上生成预测。

  2. 绘制预测值与实际值的相关性图。

  3. 绘制残差的分布图。

  4. 计算指标，然后将其放入数据框并打印出来。

    注意

    这个活动的解决方案可以在第 352 页找到。

随机森林回归模型似乎表现不如多元线性回归，这一点通过更大的 MAE、MSE 和 RMSE 值以及较低的解释方差得到了证实。此外，预测值与实际值之间的相关性较弱，残差也远未呈正态分布。然而，通过利用随机森林回归器的集成方法，我们构建了一个模型，该模型解释了 75.8%的温度方差，并预测摄氏温度±3.781 度。

总结

本章介绍了 Python 的开源机器学习库 scikit-learn。你学习了如何预处理数据，以及如何调整和拟合几种不同的回归和分类算法。最后，你学习了如何快速有效地评估分类和回归模型的性能。这是对 scikit-learn 库的全面介绍，在这里使用的策略可以应用于构建 scikit-learn 提供的众多其他算法。

在下一章，你将学习降维和无监督学习。

第十四章：第四章

降维和无监督学习

学习目标

在本章结束时，您将能够：

  • 比较层次聚类分析（HCA）和 k-means 聚类

  • 进行层次聚类分析（HCA）并解读输出结果

  • 调整 k-means 聚类的聚类数

  • 选择一个最佳的主成分数进行降维

  • 使用线性判别分析（LDA）进行监督式降维

本章将介绍降维和无监督学习下的各种概念。

介绍

在无监督学习中，描述性模型用于探索性分析，以揭示未标记数据中的模式。无监督学习任务的例子包括聚类算法和降维算法。在聚类中，观察值被分配到组中，其中组内同质性高而组间异质性大。简而言之，观察值被归类到与其他非常相似的观察值的样本群体中。聚类算法的应用场景广泛。例如，分析师通过根据顾客的购物行为将顾客分开，进而为特定顾客群体定向营销广告和促销活动，从而提高销售额。

注意

此外，层次聚类已被应用于学术神经科学和运动行为研究（https://www.researchgate.net/profile/Ming-Yang_Cheng/project/The-Effect-of-SMR-Neurofeedback-Training-on-Mental-Representation-and-Golf-Putting-Performance/attachment/57c8419808aeef0362ac36a5/AS:401522300080128@1472741784217/download/Schack±+2012±+Measuring+mental+representations.pdf?context=ProjectUpdatesLog），而 k-means 聚类已被用于欺诈检测（https://www.semanticscholar.org/paper/Fraud-Detection-in-Credit-Card-by-Clustering-Tech/3e98a9ac78b5b89944720c2b428ebf3e46d9950f）。

然而，在构建描述性或预测性模型时，确定哪些特征应纳入模型以提高模型效果，以及哪些特征应排除因为它们会削弱模型，可能是一个挑战。特征过多可能会导致问题，因为模型中变量的数量越多，多重共线性和模型过拟合的可能性就越高。此外，过多的特征增加了模型的复杂性，并延长了模型调优和拟合的时间。

当数据集变大时，这会变得更加棘手。幸运的是，另一种无监督学习的应用场景是通过创建原始特征的组合来减少数据集中的特征数量。减少数据中的特征数量有助于消除多重共线性，并汇聚出一组特征组合，从而生成一个在未见测试数据上表现良好的模型。

注意

多重共线性是指至少有两个变量之间存在相关性。这在回归模型中是一个问题，因为它无法孤立地描述每个独立变量与结果变量之间的关系。因此，系数和 p 值变得不稳定，且精确度较低。

在本章中，我们将介绍两种广泛使用的无监督聚类算法：层次聚类分析（HCA）和k 均值聚类。此外，我们还将探索使用*主成分分析（PCA）进行降维，并观察降维如何改善模型性能。最后，我们将实现线性判别函数分析(LDA)*用于监督式降维。

层次聚类分析（HCA）

层次聚类分析（HCA）最适用于用户不知道预先聚类数量的情况。因此，HCA 常作为其他聚类技术的前驱方法，其中建议使用预定数量的聚类。HCA 的工作原理是将相似的观测值合并成聚类，并继续合并距离最近的聚类，直到所有观测值合并为一个单一的聚类。

HCA 通过计算观测值之间的欧几里得距离来确定相似性，并根据两个点之间的距离建立链接。

使用特征数* n *表示，欧几里得距离的计算公式如下：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_01.jpg

图 4.1: 欧几里得距离

在计算了观测值和聚类之间的距离后，通过树状图显示所有观测值之间的关系。树状图是类似树的结构，通过水平线表示链接之间的距离。

Thomas Schack 博士（链接）将这种结构与人脑相联系，在人脑中，每个观测值都是一个节点，观测值之间的链接则是神经元。

这创建了一个层次结构，其中关系紧密的项目会被“打包”到一起，形成聚类。这里展示了一个示例树状图：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_02.jpg

](https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_02.jpg)

图 4.2: 一个示例树状图

y 轴表示欧几里得距离，x 轴表示每个观察值的行索引。水平线表示观察值之间的连接，越接近 x 轴的连接表示越短的距离及其更紧密的关系。在此示例中，似乎有三个聚类。第一个聚类包含绿色标记的观察值，第二个聚类包含红色标记的观察值，第三个聚类包含青绿色标记的观察值。

练习 34：构建 HCA 模型

为了演示 HCA，我们将使用加利福尼亚大学欧文分校（https://github.com/TrainingByPackt/Data-Science-with-Python/tree/master/Chapter04）提供的适配版本的玻璃数据集。该数据集包含 218 个观察值和 9 个特征，对应于玻璃中各种氧化物的质量百分比：

  • RI：折射率

  • Na：钠的质量百分比

  • Mg：镁的质量百分比

  • Al：铝的质量百分比

  • Si：硅的质量百分比

  • K：钾的质量百分比

  • Ca：钙的质量百分比

  • Ba：钡的质量百分比

  • Fe：铁的质量百分比

在这个练习中，我们将使用折射率（RI）和每种氧化物的质量百分比来对玻璃类型进行分段。

  1. 首先，我们将导入 pandas 并使用以下代码读取glass.csv文件：

    import pandas as pd
df = pd.read_csv('glass.csv')

  2. 通过使用以下代码打印df.info()到控制台，查看一些基本的 DataFrame 信息：

    print(df.info()):

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_03.jpg

    图 4.3：DataFrame 信息

  3. 为了去除数据中的可能的顺序效应，我们将在构建任何模型之前打乱行，并将其保存为新的数据框对象，如下所示：

    from sklearn.utils import shuffle
df_shuffled = shuffle(df, random_state=42)

  4. 通过拟合并转换打乱后的数据，使用以下方法将每个观察值转换为 z 分数：

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() 
scaled_features = scaler.fit_transform(df_shuffled)

  5. 使用scaled_features执行分层聚类，使用连接函数。以下代码将向你展示如何操作：

    from scipy.cluster.hierarchy import linkage 
model = linkage(scaled_features, method='complete')

恭喜！你已成功构建 HCA 模型。

练习 35：绘制 HCA 模型并分配预测标签

现在 HCA 模型已经构建完成，我们将继续分析，使用树状图可视化聚类，并利用该可视化生成预测。

  1. 通过绘制连接模型来显示树状图，如下所示：

    import matplotlib.pyplot as plt 
from scipy.cluster.hierarchy import dendrogram
plt.figure(figsize=(10,5))
plt.title('Dendrogram for Glass Data')
dendrogram(model, leaf_rotation=90, leaf_font_size=6)
plt.show()

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_04.jpg

    图 4.4：玻璃数据的树状图
    注意

    数据集中的每个观察值或行的索引在 x 轴上。欧几里得距离在 y 轴上。水平线表示观察值之间的连接。默认情况下，scipy 会为它找到的不同聚类进行颜色编码。

    现在我们已经得到了预测的观察值聚类，我们可以使用fcluster函数生成一个标签数组，该数组与df_shuffled中的行对应。

  2. 使用以下代码生成预测的标签，表示一个观察值属于哪个聚类：

    from scipy.cluster.hierarchy import fcluster
labels = fcluster(model, t=9, criterion='distance')

  3. 使用以下代码将标签数组作为一列添加到打乱的数据中，并预览前五行：

    df_shuffled['Predicted_Cluster'] = labels
print(df_shuffled.head(5))

  4. 查看下图中的输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_05.jpg

](https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_05.jpg)

图 4.5：在预测与观察值匹配后，df_shuffled 的前五行数据。

我们已经成功地学习了监督学习与无监督学习的区别，如何构建 HCA 模型，如何可视化和解释 HCA 的树状图，以及如何将预测的聚类标签分配给相应的观察值。

在这里，我们使用 HCA 将数据分成了三组，并将观察值与其预测的聚类匹配起来。HCA 模型的一些优点包括：

  • 它们容易构建

  • 无需提前指定聚类的数量

  • 可视化结果容易理解

然而，HCA 的一些缺点包括：

  • 终止标准的模糊性（即何时最终确定聚类数量）

  • 一旦做出聚类决策，算法无法进行调整

  • 在大数据集且特征较多的情况下，构建 HCA 模型可能会非常耗费计算资源

接下来，我们将为您介绍另一种聚类算法——K-means 聚类。该算法通过能够在初始生成聚类后进行调整，解决了 HCA 的一些不足。它比 HCA 更加节省计算资源。

K-means 聚类

与 HCA 相似，K-means 也使用距离将未标记数据的观察值分配到聚类中。然而，与 HCA 将观察值相互连接不同，K-means 会将观察值分配到 k（用户定义数量）个聚类中。

为了确定每个观察值所属的聚类，K-means 会随机生成聚类中心，并将观察值分配到其欧几里得距离与聚类中心最接近的聚类中。类似于人工神经网络中的起始权重，聚类中心是随机初始化的。在聚类中心被随机生成后，算法分为两个阶段：

  • 指派阶段

  • 更新阶段

    注意

    随机生成的聚类中心非常重要，我们将在本章稍后进行讨论。有人认为这种随机生成聚类中心的方式是算法的弱点，因为在对相同数据拟合相同模型时，结果会有所不同，且无法确保将观察值分配到合适的聚类。我们可以通过利用循环的强大功能将其转化为优势。

在指派阶段，观察值会被分配到距离它最近的聚类，如下图所示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_06.jpg

图 4.6：观察值的散点图以及用星号、三角形和菱形表示的聚类中心。

接下来，在更新阶段，聚类中心会移动到该聚类中各点的均值位置。这些聚类均值被称为质心，如下图所示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_07.jpg

图 4.7：聚类中心向质心移动。

然而，一旦计算出质心，由于某些观察比以前的聚类中心更接近新的质心，这些观察将被重新分配到不同的聚类。因此，模型必须再次更新其质心。此过程在下图中展示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_08.jpg

图 4.8：观察重新分配后质心的更新。

更新质心的过程持续进行，直到没有进一步的观察重新分配。最终的质心如下图所示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_09.jpg

图 4.9：最终质心位置和聚类分配。

使用与练习 34中相同的玻璃数据集，构建 HCA 模型，我们将拟合一个具有用户定义聚类数量的 K-Means 模型。接下来，由于质心的选择具有随机性，我们将通过构建一个具有给定聚类数量的 K-Means 模型集成，并将每个观察分配给预测聚类的众数，从而提高我们预测的可靠性。之后，我们将通过监控平均惯性（或聚类内平方和）随聚类数量的变化，来调节最佳的聚类数，并找出增加聚类数时，惯性减少的临界点。

练习 36：拟合 K-Means 模型并分配预测

由于我们的数据已经准备好（请参见练习 34，构建 HCA 模型），并且我们理解 K-Means 算法背后的概念，我们将学习如何轻松地拟合 K-Means 模型，生成预测，并将这些预测分配到相应的观察。

在导入、打乱和标准化玻璃数据集后：

  1. 使用以下代码实例化一个 KMeans 模型，假设聚类数为任意数，这里为两个聚类：

    from sklearn.cluster import KMeans
model = KMeans(n_clusters=2)

  2. 使用以下代码行将模型拟合到 scaled_features：

    model.fit(scaled_features)

  3. 使用以下代码将模型的聚类标签保存到数组 labels 中：

    labels = model.labels_

  4. 生成标签的频率表：

    import pandas as pd
pd.value_counts(labels)

    为了更好地理解，请参见以下截图：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_10.jpg

    图 4.10：两个聚类的频率表

    使用两个聚类，将 61 个观察分配到第一个聚类，157 个观察分配到第二个聚类。

  5. 使用以下代码将标签数组作为 ‘预测聚类’ 列添加到 df_shuffled 数据框中，并预览前五行：

    df_shuffled['Predicted_Cluster'] = labels
print(df_shuffled.head(5))

  6. 查看以下图中的输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_11.jpg

图 4.11：df_shuffled 的前五行

活动 12：集成 K-Means 聚类与预测计算

当算法使用随机性作为寻找最佳解决方案的一部分时（即在人工神经网络和 k-means 聚类中），在相同数据上运行相同的模型可能会得出不同的结论，从而限制我们对预测结果的信心。因此，建议多次运行这些模型，并使用所有模型的汇总度量（即均值、中位数和众数）生成预测。在本活动中，我们将构建 100 个 k-means 聚类模型的集成。

在导入、打乱和标准化玻璃数据集之后（请参见 练习 34，构建 HCA 模型）：

  1. 实例化一个空数据框架，以便为每个模型附加标签，并将其保存为新的数据框架对象 labels_df。

  2. 使用 for 循环，迭代 100 个模型，在每次迭代时将预测标签作为新列附加到 labels_df 中。计算 labels_df 中每行的众数，并将其作为新列保存到 labels_df 中。输出应如下所示：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_12.jpg

图 4.12：labels_df 的前五行
注意

本活动的解答可以在第 356 页找到。

通过迭代多个模型并在每次迭代中保存预测结果，我们极大地提高了对预测结果的信心，并将最终预测结果作为这些预测的众数。然而，这些预测是由使用预定聚类数的模型生成的。除非我们事先知道聚类数，否则我们需要发现最佳的聚类数来分割我们的观测数据。

练习 37：通过 n_clusters 计算平均惯性

k-means 算法通过最小化簇内平方和（或惯性）来将观测数据分组到不同的簇中。因此，为了提高我们对 k-means 模型的聚类数调优的信心，我们将把在 活动 12，集成 k-means 聚类与计算预测 中创建的循环（经过少许调整）放入另一个循环中，后者将迭代一个 n_clusters 范围。这会创建一个嵌套循环，迭代 10 个 n_clusters 的可能值，并在每次迭代时构建 100 个模型。在 100 次内层迭代中的每一次中，模型惯性将被计算出来。对于 10 次外层迭代中的每一次，将计算 100 个模型的平均惯性，从而得出每个 n_clusters 值的平均惯性值。

在导入、打乱和标准化玻璃数据集之后（请参见 练习 34，构建 HCA 模型）：

  1. 如下所示，在循环外部导入我们所需的包：

    from sklearn.cluster import KMeans
import numpy as np

  2. 从内到外构建和理解嵌套循环会更容易。首先，实例化一个空列表 inertia_list，我们将在内部循环的每次迭代后将惯性值附加到该列表，如下所示：

    inertia_list = []

  3. 在 for 循环中，我们将使用以下代码迭代 100 个模型：

    for i in range(100):

  4. 在循环内部，构建一个 KMeans 模型，使用 n_clusters=x，如下所示：

    model = KMeans(n_clusters=x)
    注意

    x 的值由外部 for 循环确定，我们还没有讲解这个部分，但很快会详细介绍。

  5. 如下所示，将模型拟合到 scaled_features：

    model.fit(scaled_features)

  6. 获取惯性值并将其保存为对象惯性，如下所示：

    inertia = model.inertia_

  7. 使用以下代码将惯性添加到 inertia_list 中：

    inertia_list.append(inertia)

  8. 移动到外部循环，实例化另一个空列表来存储平均惯性值，如下所示：

    mean_inertia_list = []

  9. 使用以下代码循环遍历 n_clusters 从 1 到 10 的值：

    for x in range(1, 11):

  10. 在内部 for 循环运行完 100 次迭代，并将 100 个模型的惯性值添加到 inertia_list 后，计算该列表的均值并保存为对象 mean_inertia，如下面所示：

    mean_inertia = np.mean(inertia_list)

  11. 如下所示，将 mean_inertia 添加到 mean_inertia_list 中：

    mean_inertia_list.append(mean_inertia)

  12. 在完成 100 次迭代并进行 10 次，合计 1000 次迭代后，mean_inertia_list 包含 10 个值，这些值是每个 n_clusters 值的平均惯性值。

  13. 按如下代码打印 mean_inertia_list。这些值在下图中显示：

    print(mean_inertia_list)

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_13.jpg

图 4.13：mean_inertia_list

练习 38：按 n_clusters 绘制均值惯性

继续进行练习 38：

现在我们已经为每个 n_clusters 值生成了 100 个模型的均值惯性，接下来我们将按 n_clusters 绘制均值惯性。然后，我们将讨论如何从视觉上评估选择 n_clusters 的最佳值。

  1. 首先，按如下方式导入 matplotlib：

    import matplotlib.pyplot as plt

  2. 创建一个数字列表并将其保存为对象 x，以便在 x 轴上绘制，如下所示：

    x = list(range(1, len(mean_inertia_list)+1))

  3. 将 mean_inertia_list 保存为对象 y，如下所示：

    y = mean_inertia_list

  4. 如下所示，按聚类数量绘制均值惯性：

    plt.plot(x, y)

  5. 使用以下代码将图表标题设置为 ‘Mean Inertia by n_clusters’：

     plt.title('Mean Inertia by n_clusters')

  6. 使用 plt.xlabel('n_clusters') 将 x 轴标签标记为 ‘n_clusters’，使用以下代码将 y 轴标签标记为 ‘Mean Inertia’：

    plt.ylabel ('Mean Inertia')

  7. 使用以下代码将 x 轴的刻度标签设置为 x 中的值：

    plt.xticks(x)

  8. 使用 plt.show() 显示图表。为了更好地理解，参见以下代码：

    plt.plot(x, y)
plt.title('Mean Inertia by n_clusters')
plt.xlabel('n_clusters')
plt.xticks(x)
plt.ylabel('Mean Inertia')
plt.show()

    对于结果输出，请参见以下截图：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_14.jpg

图 4.14：按 n_clusters 计算的均值惯性

为了确定最佳的 n_clusters 数量，我们将使用“肘部法则”。即在图中，随着聚类数量增加，新增聚类带来的复杂度增加，而均值惯性减少的幅度逐渐减缓。从图 4.14 中可以看出，从 n_clusters 为 1 到 3 时，均值惯性急剧下降。而当 n_clusters 等于 3 后，均值惯性的下降似乎变得缓慢，并且惯性减少可能不足以抵消增加额外聚类的复杂性。因此，在这种情况下，合适的 n_clusters 数量是 3。

然而，如果数据的维度过多，k-means 算法可能会受到维度灾难的影响，因为欧几里得距离膨胀，导致结果错误。因此，在拟合 k-Means 模型之前，建议使用降维策略。

降低维度有助于消除多重共线性，并减少拟合模型的时间。主成分分析（PCA）是一种常见的降维方法，通过发现数据中一组潜在的线性变量来减少维度。

主成分分析（PCA）

从高层次来看，PCA 是一种通过原始特征创建不相关线性组合的技术，这些组合被称为主成分。在主成分中，第一个成分解释了数据中最大比例的方差，而后续的成分则逐渐解释较少的方差。

为了演示 PCA，我们将：

  • 使用所有主成分拟合 PCA 模型

  • 通过设置解释方差的阈值来调整主成分的数量，以便保留数据中的信息。

  • 将这些成分拟合到 k-means 聚类分析中，并比较 PCA 转换前后 k-means 的性能

练习 39：拟合 PCA 模型

在本练习中，您将学习如何使用我们在练习 34：构建 HCA 模型中准备的数据和 PCA 简要说明来拟合一个通用的 PCA 模型。

  1. 按照以下方式实例化 PCA 模型：

    from sklearn.decomposition import PCA
model = PCA()

  2. 将 PCA 模型拟合到scaled_features，如下代码所示：

    model.fit(scaled_features)

  3. 获取数据中每个主成分的解释方差比例，将数组保存为对象explained_var_ratio，并将值打印到控制台，如下所示：

    explained_var_ratio = model.explained_variance_ratio_
print(explained_var_ratio)

  4. 对于结果输出，请参阅以下屏幕截图：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_15.jpg

图 4.15：每个主成分的数据解释方差

每个主成分解释了数据中的一部分方差。在本练习中，第一个主成分解释了数据中 35%的方差，第二个主成分解释了 25%，第三个主成分解释了 13%，依此类推。总的来说，这九个成分解释了数据中 100%的方差。降维的目标是减少数据中的维度，以限制过拟合和后续模型拟合的时间。因此，我们不会保留所有九个成分。然而，如果我们保留的成分太少，数据中的解释方差比例将很低，后续模型将出现欠拟合。因此，数据科学家的挑战在于确定最小化过拟合和欠拟合的n_components数量。

练习 40：使用解释方差阈值选择 n_components

在练习 39，拟合 PCA 模型中，你学会了用所有可用的主成分拟合 PCA 模型。然而，保留所有主成分并不会减少数据的维度。在本练习中，我们将通过保留解释一定方差阈值的主成分来减少数据的维度。

  1. 通过计算每个主成分解释的方差的累计和，确定最少 95%数据方差由多少个主成分解释。让我们看以下代码，看看它是如何实现的：

    import numpy as np
cum_sum_explained_var = np.cumsum(model.explained_variance_ratio_)
print(cum_sum_explained_var)

    对于结果输出，请参考以下截图：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_16.jpg

    图 4.16：每个主成分的解释方差的累计和

  2. 将数据中保持的方差百分比阈值设置为 95%，如下所示：

    threshold = .95

  3. 使用这个阈值，我们将遍历累计解释方差的列表，看看它们是否解释了数据中不少于 95%的方差。由于我们将循环遍历cum_sum_explained_var的索引，因此我们将使用以下方式实例化我们的循环：

    for i in range(len(cum_sum_explained_var)):

  4. 检查cum_sum_explained_var中的项是否大于或等于 0.95，如下所示：

    if cum_sum_explained_var[i] >= threshold:

  5. 如果满足该逻辑，则我们将在该索引上加 1（因为我们不能有 0 个主成分），将值保存为一个对象，并退出循环。为此，我们将在 if 语句中使用best_n_components = i+1，并在下一行执行 break。看看以下代码，了解如何操作：

    best_n_components = i+1
break

    if 语句中的最后两行指示循环如果逻辑不满足时不做任何操作：

    else:
pass

  6. 使用以下代码打印一条消息，详细说明最佳的主成分数量：

    print('The best n_components is {}'.format(best_n_components))

    查看上一行代码的输出：

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_17.jpg

图 4.17：显示组件数量的输出信息

best_n_components的值为 6。我们可以用n_components = 6重新拟合一个 PCA 模型，将数据转换为主成分，并在新的 k-means 模型中使用这些主成分来降低惯性值。此外，我们可以将使用 PCA 变换后的数据构建的模型与使用未经 PCA 变换的数据构建的模型在n_clusters值上的惯性值进行比较。

活动 13：通过 PCA 变换后按聚类评估平均惯性

现在我们知道了保留至少 95%数据方差的主成分数量，知道如何将特征转换为主成分，并且有了一个方法来通过嵌套循环调整 k-means 聚类的最优聚类数量，接下来我们将在这个活动中将它们整合起来。

接着进行练习 40：

  1. 使用n_components参数等于best_n_components的值实例化 PCA 模型（也就是说，记住，best_n_components = 6）。

  2. 将模型拟合到scaled_features并将其转换为前六个主成分

  3. 使用嵌套循环，计算在n_clusters值从 1 到 10 之间的 100 个模型的均值惯性（参见练习 40，使用方差解释阈值选择 n_components）。

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_18.jpg

图 4.18：mean_inertia_list_PCA

现在，就像在练习 38中所做的那样，按 n_clusters 绘制均值惯性，我们有每个n_clusters值（1 到 10）的均值惯性值。然而，mean_inertia_list_PCA包含 PCA 变换后每个n_clusters值的均值惯性值。但是，我们如何知道 PCA 变换后 k-means 模型的表现是否更好呢？在下一个练习中，我们将视觉对比每个n_clusters值下 PCA 变换前后的均值惯性。

注意

本活动的解答可以在第 357 页找到。

练习 41：按 n_clusters 进行惯性视觉对比

为了视觉对比 PCA 变换前后的均值惯性，我们将稍微修改在练习 38，按 n_clusters 绘制均值惯性中创建的图表，方法如下：

  • 向图表中添加一条显示 PCA 变换后按n_clusters绘制的均值惯性曲线

  • 创建一个图例来区分各条线

  • 更改标题

    注意

    为了让这个可视化正常工作，练习 38中的mean_inertia_list，按 n_clusters 绘制均值惯性，必须仍然存在于环境中。

继续进行活动 13：

  1. 使用以下代码导入 Matplotlib：

    import matplotlib.pyplot as plt

  2. 创建一个数字列表并将其保存为对象 x，以便我们可以在 x 轴上绘制，方法如下：

    x = list(range(1,len(mean_inertia_list_PCA)+1))

  3. 使用以下代码将mean_inertia_list_PCA保存为对象 y：

    y = mean_inertia_list_PCA

  4. 使用以下代码将mean_inertia_list保存为对象 y2：

    y2 = mean_inertia_list

  5. 使用以下代码按聚类数绘制 PCA 变换后的均值惯性：

    plt.plot(x, y, label='PCA')

    使用以下方法在 PCA 变换之前，按聚类数添加我们的第二条均值惯性线：

    plt.plot(x, y2, label='No PCA)

  6. 将图表标题设置为’Mean Inertia by n_clusters for Original Features and PCA Transformed Features’，如下所示：

    plt.title('Mean Inertia by n_clusters for Original Features and PCA Transformed Features')

  7. 使用以下代码将 x 轴标签标记为’n_clusters’：

    plt.xlabel('n_clusters')

  8. 使用以下代码将 y 轴标签标记为’Mean Inertia’：

    plt.ylabel('Mean Inertia')

  9. 使用plt.xticks(x)将 x 轴的刻度标签设置为 x 中的值。

  10. 使用并显示图表如下所示，显示图例：

    plt.legend()
plt.show()

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_19.jpg

图 4.19：原始特征（橙色）和 PCA 变换特征（蓝色）按 n_clusters 的均值惯性

从图表中，我们可以看到，在模型中使用 PCA 转换后的特征时，每个聚类数的惯性较低。这表明，在 PCA 转换后，相比于转换前，各聚类的组质心与观测值之间的距离更小。因此，通过对原始特征进行 PCA 转换，我们能够减少特征数量，并同时通过减少组内平方和（即惯性）来改进我们的模型。

HCA 和 k-means 聚类是两种广泛使用的无监督学习技术，用于数据分割。PCA 可用于帮助减少数据维度，并以无监督的方式改进模型。而线性判别函数分析（LDA）则是一种监督方法，通过数据压缩来减少维度。

使用线性判别分析（LDA）进行监督数据压缩

如前所述，PCA 将特征转换为一组最大化特征间方差的变量。在 PCA 中，输出标签在拟合模型时不被考虑。与此同时，LDA 使用因变量来帮助将数据压缩成能最好区分结果变量类别的特征。在这一部分中，我们将演示如何使用 LDA 作为监督数据压缩技术。

为了演示如何使用 LDA 作为监督的降维压缩技术，我们将：

  • 使用所有可能的 n_components 拟合一个 LDA 模型

  • 将我们的特征转换为 n_components

  • 调整 n_components 的数量

练习 42：拟合 LDA 模型

为了使用 LDA 算法的默认参数将模型作为监督学习者拟合，我们将使用一个稍有不同的玻璃数据集，glass_w_outcome.csv。（https://github.com/TrainingByPackt/Data-Science-with-Python/tree/master/Chapter04）此数据集包含与玻璃数据集相同的九个特征，但还包括一个结果变量 Type，表示玻璃的类型。Type 被标记为 1、2 和 3，分别对应建筑窗户浮法处理、建筑窗户非浮法处理和车灯。

  1. 导入 glass_w_outcome.csv 文件，并使用以下代码将其保存为对象 df：

    import pandas as pd
df = pd.read_csv(‘glass_w_outcome.csv’)

  2. 打乱数据以消除任何顺序效应，并将其保存为数据框 df_shuffled，如下所示：

    from sklearn.utils import shuffle
df_shuffled = shuffle(df, random_state=42)

  3. 将 Type 保存为 DV（即，因变量），如下所示：

    DV = ‘Type’

  4. 使用 X = df_shuffled.drop(DV, axis=1) 和 y = df_shuffled[DV] 将打乱后的数据拆分为特征（即 X）和结果（即 y）。

  5. 按照如下方式将 X 和 y 拆分为测试集和训练集：

    from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

  6. 使用以下代码分别对 X_train 和 X_test 进行缩放：

    from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() 
X_train_scaled = scaler.fit_transform(X_train) 
X_test_scaled = scaler.fit_transform(X_test)

  7. 实例化 LDA 模型并将其保存为模型。以下将向您展示如何操作。

    from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
-model = LinearDiscriminantAnalysis()
    注意

    通过实例化一个不带参数 for n_components 的 LDA 模型，我们将返回所有可能的成分。

  8. 使用以下代码将模型拟合到训练数据：

    model.fit(X_train_scaled, y_train)

  9. 请参见下面的结果输出：![图 4.20：线性判别函数分析的拟合结果输出]

    ](https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_20.jpg)

    图 4.20：拟合线性判别分析函数后的输出

  10. 与 PCA 类似，我们可以返回每个组件解释的方差百分比。

    model.explained_variance_ratio_

    输出如下图所示。

https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_21.jpg

图 4.21：按组件解释的方差。
注意

第一个组件解释了数据中 95.86% 的方差，第二个组件解释了数据中 4.14% 的方差，总共为 100%。

我们成功地将 LDA 模型拟合到数据中，将数据从九个特征压缩到两个特征。将特征减少到两个可以减少调优和拟合机器学习模型的时间。然而，在将这些特征应用于分类器模型之前，我们必须将训练和测试特征转换为其两个组成部分。在下一个练习中，我们将展示如何实现这一过程。

练习 43：在分类模型中使用 LDA 转换的组件

通过监督式数据压缩，我们将把训练和测试特征（即 X_train_scaled 和 X_test_scaled）转换为其组成部分，并在其上拟合 RandomForestClassifier 模型。

继续进行练习 42：

  1. 将X_train_scaled压缩为其组成部分，如下所示：

    X_train_LDA = model.transform(X_train_scaled)

  2. 使用以下方式将X_test压缩为其组成部分：

    X_test_LDA = model.transform(X_test_scaled)

  3. 按如下方式实例化一个RandomForestClassifier模型：

    from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
    注意

    我们将使用RandomForestClassifier模型的默认超参数，因为超参数调优超出了本章的范围。

  4. 使用以下代码将模型拟合到压缩后的训练数据：

    model.fit(X_train_LDA, y_train)

    请参见下方的结果输出：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_22.jpg

    图 4.22：拟合随机森林分类器模型后的输出

  5. 使用以下代码在X_test_LDA上生成预测并将其保存为数组 predictions：

    predictions = model.predict(X_test_LDA)

  6. 通过将预测与 y_test 进行比较，使用混淆矩阵评估模型性能。要生成并打印混淆矩阵，请参见以下代码：

    from sklearn.metrics import confusion_matrix 
import pandas as pd
import numpy as np
cm = pd.DataFrame(confusion_matrix(y_test, predictions))
cm[‘Total’] = np.sum(cm, axis=1)
cm = cm.append(np.sum(cm, axis=0), ignore_index=True)
cm.columns = [‘Predicted 1’, ‘Predicted 2’, ‘Predicted 3’, ‘Total’]
cm = cm.set_index([[‘Actual 1’, ‘Actual 2’, ‘Actual 3’, ‘Total’]])
print(cm)

    输出如下图所示：

    https://github.com/OpenDocCN/freelearn-ds-pt5-zh/raw/master/docs/ds-py/img/C13322_04_23.jpg

图 4.23：使用 LDA 压缩数据评估随机森林分类器模型性能的 3x3 混淆矩阵

总结

本章向你介绍了两种广泛使用的无监督聚类算法——HCA 和 k-means 聚类。在学习 k-means 聚类时，我们利用循环的力量创建了多个模型集，以调节聚类的数量，并提高我们预测的可靠性。在 PCA 部分，我们确定了用于降维的主成分数量，并将这些成分拟合到 k-means 模型中。此外，我们比较了 PCA 转换前后 k-means 模型性能的差异。我们还介绍了一种算法——LDA，它以监督方式减少维度。最后，我们通过遍历所有可能的成分值，并通过编程返回使得随机森林分类器模型获得最佳准确度得分的值，来调节 LDA 中的成分数量。现在，你应该已经对降维和无监督学习技术感到得心应手。

本章简要介绍了如何创建图表；然而，在下一章，我们将学习结构化数据以及如何使用 XGboost 和 Keras 库。

Logo
量化交易与投资社区

专业量化交易与投资者大本营

更多推荐

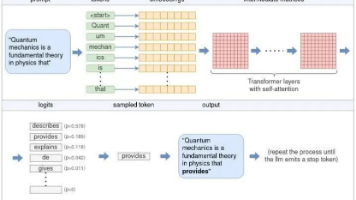
cover

Python机器学习：从零基础到项目实战

avatar 量化交易与投资社区
cover

Deepseek大模型推理算法其实很简单，零基础入门到精通，收藏这一篇就够了

avatar 量化交易与投资社区
cover

计算机就业前景较好的五个专业，毕业后容易拿高薪，有你学的吗？

avatar 量化交易与投资社区