第 14 章 线性回归预测策略----SPL量化编程课
线性回归模型在股票量化策略中的应用:本文介绍了基于线性代数的回归分析在股市预测中的使用方法。通过建立以财务指标或价格数据为自变量、股票价格为因变量的线性模型,可实现对股价走势的预测。文章详细阐述了建模步骤,包括训练/预测数据划分、PCA降维处理共线性问题等关键环节,并提供了Spl代码实现。实际测试表明,单纯依赖线性回归模型预测效果有限,建议结合其他指标综合判断。文中强调数学建模时需注意共线性问题,
基于线性代数的回归分析也是量化策略中常用到的数学工具,我们来尝试一下,并了解其中的一些注意事项。
在股市投资中,投资者往往需要根据历史数据来预测未来的市场趋势,以便做出更明智的投资决策。线性回归作为一种经典的统计工具,在股票量化策略中发挥着举足轻重的作用,它通过对历史数据进行统计分析,建立出一个尽可能反映市场规律的模型,从而预测未来的股票价格走势。
线性回归的基本原理是找出一个最适合的直线(这条直线也称为模型),使这条直线能够最好地拟合给定的数据点。这条直线通常被称为“回归线”,它的公式如下:
y = a + bx
其中,y 是因变量(股票价格),x 是自变量(如历史价格、历史财务指标等),a 和 b 是待求解的参数。
例如,我们可以选取公司的市盈率、市净率、营业收入增长率等财务指标作为自变量,股票价格作为因变量,建立线性回归模型。通过对大量历史数据的拟合,可以得到这些财务指标与股票价格之间的线性关系方程。在未来,当我们知道了这些财务指标的值时,就可以通过这个方程来预测股票价格的大致范围。
再例如,通过对过去一段时间内股票价格的变化进行线性回归分析,可以得到价格变化的趋势线。如果趋势线向上倾斜,说明股票价格处于上升趋势;如果趋势线向下倾斜,说明股票价格处于下降趋势。
需要注意的是线性回归算法提供了一种预测股票价格的方法,但并不能保证 100% 的准确性。因此,在使用线性回归模型时,需要结合其他信息和个人判断,制定出更全面的投资策略。此外,还需要定期对模型进行验证和调整,以适应市场的变化。
本章我们将编写一个通用的线性模型函数,使用时用户只要传入自己的数据,修改个别参数就可以建立任意模型。
建立线性模型的主要思路为:
1. 确定自变量和因变量。因变量一般就是每日的股票价格,如收盘价;自变量可以是价格、财务指标、量化因子等等。
2. 确定训练数据和预测数据的天数,取前 n 天数据做训练,近 m 天数据做预测。例如取前 n 天数据训练,近 m 天数据预测
3. 对自变量特征进行 PCA 主成分分析,提取前 k 个主要成分。这是因为在进行线性拟合时要求自变量之间相互独立,而在历史数据中多个变量之间经常会出现一定程度(甚至高度)的相关性,称为共线性,共线性会导致拟合时参数的估计值变的不稳定。而 PCA 是一种常用的降维方法,它能将许多相关性很高的变量转化成少数几个彼此相互独立或不相关的变量。如果不做降维处理,线性回归的结果会对历史数据吻合相当好,而对于未来数据完全无效。回顾一下中学学过的多元一次方程,如果自变量个数大于方程数量,则会有无穷多组可行解,这样的方程组就没有意义了。PCA 方法的本质就是把自变量的数量降低到小于方程数量,这时候回归拟合才有意义。这是使用数学方法做预测模型时特别需要关注的环节。
4. 降维之后,就可以用 linefit() 函数做线性回归的预测模型了。
5. 在预测数据上做预测,得到第二天的股票价格
根据这个思路我们来编写线性回归指标函数。
定义指标参数:
| A | 序表,包含自变量的K线数据 |
| y | 指标返回列,模型预测的股票价格 |
| n | 数字,训练数据天数 |
| m | 数字,预测数据天数 |
| k | 4数字,主成分个数,缺省值为 |
在indicator.splx中编写指标函数:
| A | B | |
| … | …… | …… |
| 51 | func PCALF(A, $y, n, m, k=4) | =A.derive@o(~[-m+1:0].conj([开盘,收盘,最高,最低]):PCALF0) |
| 52 |
=A.run( if( #>n+m, ( ox=PCALF0[-n:-1], tm=pca(ox, k), tx=pca(ox, tm), ty=收盘[-n+1,0], mc=linefit(tx.(~|1), ty ), d=pca([PCALF0], tm ).(~|1),${y}=mul(d, mc) ))) |
|
| 53 | =A.alter(; PCALF0) |
这段代码中 pca 函数来自于数学库,读者使用时要在工具→选项菜单中加载数学库。
B49 格中的“[开盘, 收盘, 最高, 最低]”是建模的自变量,读者可以自行修改。
有了这个指标,我们就很容易在策略中使用模型来做预测了。如果预测收盘价 > 当天的收盘价,则标记为买入信号 1;否则标记为卖出信号 -1。
| A | B | |
| 1 | >call("init.splx") | |
| 2 | 2024 | =date(A2,1,1) |
| 3 | =workday(B2,-110,HOLIDAY) | =date(A2,12,31) |
| 4 | 600690 | =Load@C(A4, A3,B3) |
| 5 | ||
| 6 | =B4.derive(:Y) | |
| 7 | =PCALF(A6, Y, 100, 5) | =A7.run( Y=sign(Y-收盘) ) |
| 8 | ||
| 9 | =Begin(A6) | |
| 10 | =A9.select(日期>=B2) | |
| 11 | for A10 | =H=昨日.持仓 |
| 12 | =卖出=if(昨日.Y==-1,SellOff( ~, H,收盘 ) ) | |
| 13 | =if(昨日.Y==1 && H.len()<=0, 买入|=Buy( ~,100,收盘)) | |
| 14 | =Loop() | |
| 15 | =Summary(A10) | =Display(A15) |
A7 调用函数预测第二天股票价格
B7 预测价格 - 当天价格,得到买入和卖出信号。
回测结果:
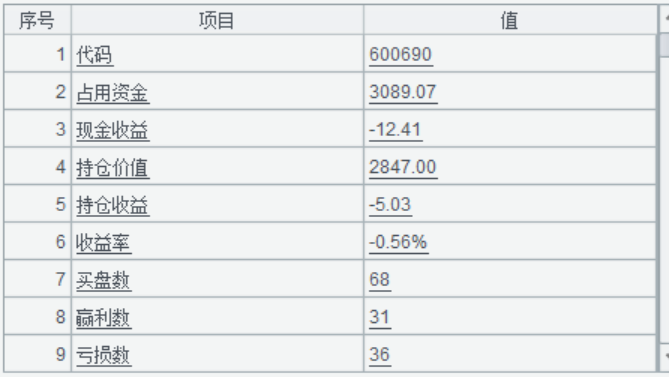
效果也不是很好,反而不如之前的朴素方案。
总结一下,从这几个例子可以看出,在指标体系框架下,只要有合适的指标,即使看起来很复杂的策略也可以很容易做出来。而很多指标具备通用性,开发后可以一劳永逸。在本书的附录部分我们也会提供一些常用的指标函数,方便读者使用。
更多推荐
 已为社区贡献18条内容
已为社区贡献18条内容








所有评论(0)