RSRS（二）四种基于RSRS指标的策略回测研究

平台：聚宽

完整代码和数据可关注gzh’finance褪黑素’回复关键词 【3004】 免费+无套路 获取！

一、简介

RSRS（Rolling Regression Slope）策略是一种基于时间序列数据的量化交易策略，旨在利用滚动回归分析市场趋势，并根据趋势变化进行交易决策。以下是该策略涉及到的主要内容和相关公式的整合：

1. 滚动回归斜率（Rolling Regression Slope）：
   在每个时点t，使用最近N个交易日的数据进行线性回归，计算高价（high）和低价（low）之间的回归斜率（beta）。
   计算公式为：
   $${\beta }_t=\frac{{\sum }_{i=t-N+1}^t(hig{h}_i-\overline{high})(lo{w}_i-\overline{low})}{{\sum }_{i=t-N+1}^t(lo{w}_i-\overline{low}{)}^2}其中，$$

   • $hig{h}_i$ 和 $lo{w}_i$ 分别为第i个交易日的最高价和最低价；
   • $\overline{high}$和 $\overline{low}$ 分别为最近N个交易日的最高价和最低价的均值。

2. 斜率标准分数（Beta Normalized）：
   对回归斜率进行归一化处理，使得不同时间点的斜率可以进行比较。常用的方法是计算斜率与其在过去M个交易日内的均值的标准化差异。

3. RSRS指标（Rolling Regression Slope-R-squared）：
   RSRS指标是滚动回归斜率和R平方值的乘积，用于综合评估市场趋势和震荡情况。
   计算公式为：
   $$RSRS\_R{2}_t={\beta }_{norm,t}\times R_t^2$$

   • ${\beta }_{norm,t}$ 是斜率标准分数；
   • $R_t^2$ 是回归模型在第t个时点的拟合优度，即R平方值。

4. 统计分析和绘图：
   使用统计学方法（如计算均值、标准差、偏度和峰度等）对RSRS指标和其他相关指标进行分析，以及通过绘制直方图和曲线图来展示分析结果。

RSRS策略通过滚动回归计算的斜率和RSRS指标，综合考虑了市场的趋势和震荡情况，可以作为量化交易中的参考指标，用于制定交易策略和进行交易决策。

二、主要代码

import pandas as pd
import os
import datetime
import numpy as np 
import statsmodels.formula.api as sml
import matplotlib.pyplot as plt
import tushare as ts
import scipy.stats as scs
import matplotlib.mlab as mlab
#聚宽
#import statsmodels.api as sm
#from pandas.stats.api import ols

dateStart = datetime.date(2005,3,8)
dateEnd = datetime.date(2024,3,8)
HS300 = ts.get_k_data('000300', index=True,start = '{}'.format(dateStart),end = '{}'.format(dateEnd))
HS300.head()

	date	open	close	high	low	volume	code
0	2005-04-08	984.66	1003.45	1003.70	979.53	14762500.0	sh000300
1	2005-04-11	1003.88	995.42	1008.73	992.77	15936100.0	sh000300
2	2005-04-12	993.71	978.70	993.71	978.20	10226200.0	sh000300
3	2005-04-13	987.95	1000.90	1006.50	987.95	16071700.0	sh000300
4	2005-04-14	1004.64	986.97	1006.42	985.58	12945700.0	sh000300

def getdata(dateStart,dateEnd,N,M):
    HS300 = ts.get_k_data('000300', index=True,start = '{}'.format(dateStart),end = '{}'.format(dateEnd))
    HS300=HS300[['date','high','low','open','close']]

    # 斜率
    HS300['beta'] = 0
    HS300['R2'] = 0
    for i in range(1,len(HS300)-1):
        
        df_ne=HS300.loc[ i- N+1:i + 1 ,:]
        model = sml.ols(formula='high~low',data = df_ne)
        result=model.fit()

        HS300.loc[i+1,'beta'] = result.params[1]
        HS300.loc[i+1,'R2'] = result.rsquared
    # 日收益率 
    HS300['ret'] = HS300.close.pct_change(1)
    
    # 标准分
    HS300['beta_norm'] = (HS300['beta'] - HS300.beta.rolling(M).mean().shift(1))/HS300.beta.rolling(M).std().shift(1)
    for i in range(M):
        HS300.loc[i,'beta_norm'] = (HS300.loc[i,'beta'] - HS300.loc[:i-1,'beta'].mean())/HS300.loc[:i-1,'beta'].std() 
    HS300.loc[2,'beta_norm'] = 0
    HS300['RSRS_R2'] = HS300.beta_norm*HS300.R2
    HS300 = HS300.fillna(0)
    
    # 右偏标准分
    HS300['beta_right'] = HS300.RSRS_R2*HS300.beta
    return(HS300)

dateStart = datetime.date(2005,3,8)
dateEnd = datetime.date(2022,12,31)
N = 15
M = 600
HS300 = getdata(dateStart,dateEnd,N,M)
HS300.head()

	date	high	low	open	close	beta	R2	ret	beta_norm	RSRS_R2	beta_right
0	2005-04-08	1003.70	979.53	984.66	1003.45	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
1	2005-04-11	1008.73	992.77	1003.88	995.42	0.000000	0.000000	-0.008002	0.000000	0.000000	0.000000
2	2005-04-12	993.71	978.20	993.71	978.70	0.767238	0.653529	-0.016797	0.000000	0.000000	0.000000
3	2005-04-13	1006.50	987.95	987.95	1000.90	0.791216	0.687122	0.022683	1.208831	0.830615	0.657196
4	2005-04-14	1006.42	985.58	1004.64	986.97	0.804497	0.670781	-0.013917	0.921975	0.618444	0.497536

HS300 = HS300.loc[2:]
HS300 =HS300.reset_index(drop = True)
HS300.head()

	date	high	low	open	close	beta	R2	ret	beta_norm	RSRS_R2	beta_right
0	2005-04-12	993.71	978.20	993.71	978.70	0.767238	0.653529	-0.016797	0.000000	0.000000	0.000000
1	2005-04-13	1006.50	987.95	987.95	1000.90	0.791216	0.687122	0.022683	1.208831	0.830615	0.657196
2	2005-04-14	1006.42	985.58	1004.64	986.97	0.804497	0.670781	-0.013917	0.921975	0.618444	0.497536
3	2005-04-15	982.61	971.93	982.61	974.08	1.214834	0.812732	-0.013060	1.719667	1.397629	1.697887
4	2005-04-18	970.91	958.65	970.91	963.77	1.220131	0.923110	-0.010584	1.271125	1.173388	1.431687

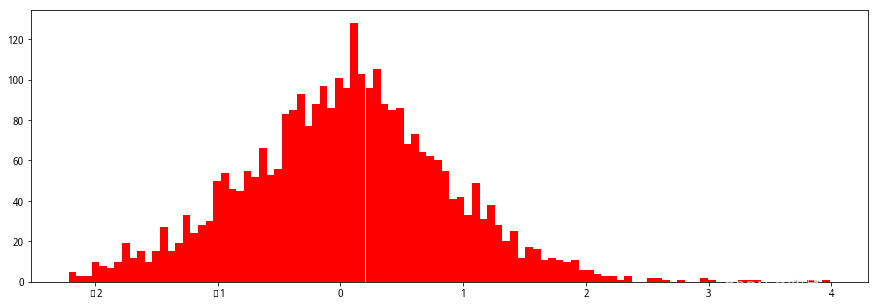
#斜率数据分布
plt.figure(figsize=(15,5))
plt.hist(HS300['beta'], bins= 100, range= None, normed= False, weights= None, cumulative= False, 
         bottom= None, histtype= 'bar', align= 'mid', orientation= 'vertical', rwidth= None, log= False, color= 'r', 
         label='直方图', stacked= False)
plt.show()

#RSRS标准分和右偏变准分分布
plt.figure(figsize=(15,5))
plt.hist(HS300['beta_norm'], bins= 100, range= None, normed= False, weights= None, cumulative= False, 
         bottom= None, histtype= 'bar', align= 'mid', orientation= 'vertical', rwidth= None, log= False, color= 'r', 
         label='直方图', stacked= False)
plt.show()

plt.figure(figsize=(15,5))
plt.hist(HS300['RSRS_R2'], bins= 100, range= None, normed= False, weights= None, cumulative= False, 
         bottom= None, histtype= 'bar', align= 'mid', orientation= 'vertical', rwidth= None, log= False, color= 'r', 
         label='直方图', stacked= False)
plt.show()

sta = scs.describe(HS300.beta)
stew = sta[4]
kurtosis = sta[5]

sta1 = scs.describe(HS300.beta_norm)
stew1 = sta1[4]
kurtosis1 = sta1[5]

sta2 = scs.describe(HS300.RSRS_R2)
stew2 = sta2[4]
kurtosis2 = sta2[5]

print('斜率的均值:%s' % (HS300['beta'].mean()))
print('斜率的标准差:%s' % (HS300['beta'].std()))
print('斜率的偏度:%s' % (stew))
print('斜率的峰度:%s' % (kurtosis))
print('')
print('斜率标准分的均值:%s' % (HS300['beta_norm'].mean()))
print('斜率标准分的标准差:%s' % (HS300['beta_norm'].std()))
print('斜率标准分的偏度:%s' % (stew1))
print('斜率标准分的峰度:%s' % (kurtosis1))
print('')
print('斜率标准分的均值:%s' % (HS300['RSRS_R2'].mean()))
print('斜率标准分的标准差:%s' % (HS300['RSRS_R2'].std()))
print('斜率标准分的偏度:%s' % (stew2))
print('斜率标准分的峰度:%s' % (kurtosis2))

斜率的均值:0.9107300548852182
斜率的标准差:0.11510992220867003
斜率的偏度:-0.37650035325581255
斜率的峰度:0.880393019660489

斜率标准分的均值:-0.02022967957717388
斜率标准分的标准差:1.0215397882843733
斜率标准分的偏度:-0.44956956799879083
斜率标准分的峰度:1.2596938448054438

斜率标准分的均值:0.04386035016941067
斜率标准分的标准差:0.8333195496560563
斜率标准分的偏度:0.13435897885521442
斜率标准分的峰度:0.4567819364025256

#斜率指标过去250天均值曲线
HS300['beta_mean'] = HS300.beta.rolling(250).mean().shift(1)
for i in range(250):
    HS300.loc[i,'beta_mean'] = HS300.loc[:i-1,'beta'].mean()

result = HS300.loc[10:].copy()
result = result.reset_index(drop = True)
xtick = np.arange(0,result.shape[0],int(result.shape[0]/7))
xticklabel = pd.Series(result.date[xtick])
plt.figure(figsize=(15,3))
fig = plt.axes()
plt.plot(np.arange(result.shape[0]),result.beta_mean,linewidth = 3,color = 'black')

fig.set_xticks(xtick)
fig.set_xticklabels(xticklabel,rotation = 45)
plt.legend()
plt.show()

三、四种策略的实现

策略一：斜率指标交易策略标准分策略

#斜率指标交易策略标准分策略
def RSRS1(HS300,S1 = 1.0,S2 = 0.8):
    data  = HS300.copy()
    data['flag'] = 0 # 买卖标记
    data['position'] = 0 # 持仓标记
    position = 0 # 是否持仓，持仓：1，不持仓：0
    for i in range(1,data.shape[0]-1):
        
        # 开仓
        if data.loc[i,'beta']>S1 and position ==0:
            data.loc[i,'flag'] = 1
            data.loc[i+1,'position'] = 1
            position = 1
        # 平仓
        elif data.loc[i,'beta']<S2 and position ==1: 
            data.loc[i,'flag'] = -1
            data.loc[i+1,'position'] = 0     
            position = 0
        
        # 保持
        else:
            data.loc[i+1,'position'] = data.loc[i,'position']     
        
    data['nav'] = (1+data.close.pct_change(1).fillna(0)*data.position).cumprod() 
        
    return(data)

策略二：标准分策略

#标准分策略

def RSRS2(HS300,S = 0.7):
    data = HS300.copy()
    data['flag'] = 0 # 买卖标记
    data['position'] = 0 # 持仓标记
    position = 0 # 是否持仓，持仓：1，不持仓：0
    for i in range(1,data.shape[0]-1):
        
        # 开仓
        if data.loc[i,'beta_norm']>S and position ==0:
            data.loc[i,'flag'] = 1
            data.loc[i+1,'position'] = 1
            position = 1
        # 平仓
        elif data.loc[i,'beta_norm']<-S and position ==1: 
            data.loc[i,'flag'] = -1
            data.loc[i+1,'position'] = 0     
            position = 0
        
        # 保持
        else:
            data.loc[i+1,'position'] = data.loc[i,'position']     
        
    data['nav'] = (1+data.close.pct_change(1).fillna(0)*data.position).cumprod() 
           
    return(data)

策略三：修正标准分策略

# 修正标准分策略
def RSRS3(HS300,S = 0.7):
    data = HS300.copy()
    data['flag'] = 0 # 买卖标记
    data['position'] = 0 # 持仓标记
    position = 0 # 是否持仓，持仓：1，不持仓：0
    for i in range(1,data.shape[0]-1):
        
        # 开仓
        if data.loc[i,'RSRS_R2']>S and position ==0:
            data.loc[i,'flag'] = 1
            data.loc[i+1,'position'] = 1
            position = 1
        # 平仓
        elif data.loc[i,'RSRS_R2']<-S and position ==1: 
            data.loc[i,'flag'] = -1
            data.loc[i+1,'position'] = 0     
            position = 0
        
        # 保持
        else:
            data.loc[i+1,'position'] = data.loc[i,'position']     
        
    data['nav'] = (1+data.close.pct_change(1).fillna(0)*data.position).cumprod() 
           
    return(data)

策略四：右偏标准分策略

#右偏标准分策略
def RSRS4(HS300,S = 0.7):
    data = HS300.copy()
    data['flag'] = 0 # 买卖标记
    data['position'] = 0 # 持仓标记
    position = 0 # 是否持仓，持仓：1，不持仓：0
    for i in range(1,data.shape[0]-1):
        
        # 开仓
        if data.loc[i,'beta_right']>S and position ==0:
            data.loc[i,'flag'] = 1
            data.loc[i+1,'position'] = 1
            position = 1
        # 平仓
        elif data.loc[i,'beta_right']<-S and position ==1: 
            data.loc[i,'flag'] = -1
            data.loc[i+1,'position'] = 0     
            position = 0
        
        # 保持
        else:
            data.loc[i+1,'position'] = data.loc[i,'position']     
        
    data['nav'] = (1+data.close.pct_change(1).fillna(0)*data.position).cumprod() 
           
    return(data)

result = RSRS1(HS300)
num = result.flag.abs().sum()/2
nav = result.nav[result.shape[0]-1]

print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  44.0
策略净值为=  11.211012175460354

xtick = np.arange(0,result.shape[0],int(result.shape[0]/7))
xticklabel = pd.Series(result.date[xtick])
plt.figure(figsize=(15,3))
fig = plt.axes()
plt.plot(np.arange(result.shape[0]),result.nav,label = 'RSRS1',linewidth = 2,color = 'red')
plt.plot(np.arange(result.shape[0]),result.close/result.close[0],color = 'yellow',label = 'HS300',linewidth = 2)

fig.set_xticks(xtick)
fig.set_xticklabels(xticklabel,rotation = 45)
plt.legend()
plt.show()

result2 = RSRS2(HS300)
num = result2.flag.abs().sum()/2
nav = result2.nav[result.shape[0]-1]
ret_year = (nav - 1)
print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  49.5
策略净值为=  9.793926481255566

result3 = RSRS3(HS300)
num = result3.flag.abs().sum()/2
nav = result3.nav[result.shape[0]-1]
ret_year = (nav - 1)
print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  44.5
策略净值为=  8.58132605273418

dateStart = datetime.date(2005,3,8)
dateEnd = datetime.date(2022,12,31)
N = 16
M = 300
HS300 = getdata(dateStart,dateEnd,N,M)
HS300 = HS300.loc[2:]
HS300 =HS300.reset_index(drop = True)

result4 = RSRS4(HS300)
num = result4.flag.abs().sum()/2
nav = result4.nav[result.shape[0]-1]
ret_year = (nav - 1)
print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  37.5
策略净值为=  9.946785407409507

xtick = np.arange(0,result.shape[0],int(result.shape[0]/7))
xticklabel = pd.Series(result.date[xtick])
plt.figure(figsize=(15,3))
fig = plt.axes()
plt.plot(np.arange(result.shape[0]),result.nav,label = 'RSRS1',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result2.nav,label = 'RSRS2',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result3.nav,label = 'RSRS3',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result4.nav,label = 'RSRS4',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result.close/result.close[0],color = 'yellow',label = 'HS300',linewidth = 2)

fig.set_xticks(xtick)
fig.set_xticklabels(xticklabel,rotation = 45)
plt.legend()
plt.show()

四种策略时间更新到当前

#四种策略时间更新到当前
dateStart = datetime.date(2005,3,1)
dateEnd = datetime.date(2024,3,8)
N = 18
M = 600
HS300 = getdata(dateStart,dateEnd,N,M)
HS300 = HS300.loc[2:]
HS300 =HS300.reset_index(drop = True)
HS300.head()

	date	high	low	open	close	beta	R2	ret	beta_norm	RSRS_R2	beta_right
0	2005-04-12	993.71	978.20	993.71	978.70	0.767238	0.653529	-0.016797	0.000000	0.000000	0.000000
1	2005-04-13	1006.50	987.95	987.95	1000.90	0.791216	0.687122	0.022683	1.208831	0.830615	0.657196
2	2005-04-14	1006.42	985.58	1004.64	986.97	0.804497	0.670781	-0.013917	0.921975	0.618444	0.497536
3	2005-04-15	982.61	971.93	982.61	974.08	1.214834	0.812732	-0.013060	1.719667	1.397629	1.697887
4	2005-04-18	970.91	958.65	970.91	963.77	1.220131	0.923110	-0.010584	1.271125	1.173388	1.431687

#斜率指标策略
result = RSRS1(HS300)
num = result.flag.abs().sum()/2
nav = result.nav[result.shape[0]-1]

print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  47.5
策略净值为=  11.833232225885457

#标准分策略
result2 = RSRS2(HS300)
num = result2.flag.abs().sum()/2
nav = result2.nav[result.shape[0]-1]
ret_year = (nav - 1)
print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  53.5
策略净值为=  10.546245684216888

#修正标准分策略
result3 = RSRS3(HS300)
num = result3.flag.abs().sum()/2
nav = result3.nav[result.shape[0]-1]
ret_year = (nav - 1)
print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  46.5
策略净值为=  9.87532821653873

dateStart = datetime.date(2005,3,1)
dateEnd = datetime.date(2019,3,8)
N = 16
M = 300
HS300 = getdata(dateStart,dateEnd,N,M)
HS300 = HS300.loc[2:]
HS300 =HS300.reset_index(drop = True)
HS300.head()

	date	high	low	open	close	beta	R2	ret	beta_norm	RSRS_R2	beta_right
0	2005-04-12	993.71	978.20	993.71	978.70	0.767238	0.653529	-0.016797	0.000000	0.000000	0.000000
1	2005-04-13	1006.50	987.95	987.95	1000.90	0.791216	0.687122	0.022683	1.208831	0.830615	0.657196
2	2005-04-14	1006.42	985.58	1004.64	986.97	0.804497	0.670781	-0.013917	0.921975	0.618444	0.497536
3	2005-04-15	982.61	971.93	982.61	974.08	1.214834	0.812732	-0.013060	1.719667	1.397629	1.697887
4	2005-04-18	970.91	958.65	970.91	963.77	1.220131	0.923110	-0.010584	1.271125	1.173388	1.431687

result4 = RSRS4(HS300)
num = result4.flag.abs().sum()/2
nav = result4.nav[result.shape[0]-1]
ret_year = (nav - 1)
print('交易次数 = ',num)
print('策略净值为= ',nav)

交易次数 =  39.5
策略净值为=  11.446891338270705

xtick = np.arange(0,result.shape[0],int(result.shape[0]/7))
xticklabel = pd.Series(result.date[xtick])
plt.figure(figsize=(15,3))
fig = plt.axes()
plt.plot(np.arange(result.shape[0]),result.nav,label = 'RSRS1',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result2.nav,label = 'RSRS2',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result3.nav,label = 'RSRS3',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result4.nav,label = 'RSRS4',linewidth = 2)
plt.plot(np.arange(result.shape[0]),result.close/result.close[0],color = 'yellow',label = 'HS300',linewidth = 2)

fig.set_xticks(xtick)
fig.set_xticklabels(xticklabel,rotation = 45)
plt.legend()
plt.show()

完整代码和数据可关注gzh’finance褪黑素’回复关键词 【3004】 免费+无套路 获取！