有感兴趣量化技术，特别是大数据、人工智能在量化中的应用的童鞋们可以关注我的公众号，脚本代码如果排版不清楚请看公众号：

馨视野（datahomex）：

       

         今天，我们回顾一下入门机器学习一文里开发的线性回归模型，看下有什么可以改进的地方，最后讲下如何将开发的模型应用到backtrader中。

一、简单回顾

        上次开发的线性回归模型主要是利用过去2周的收盘价格预测未来一周内最高的收盘价格。

from sklearn.metrics import mean_absolute_error,mean_squared_error,median_absolute_error,r2_score
y_pred_linear = lin_reg.predict(X_valid) #预测
print("平均绝对值误差:", mean_absolute_error(y_valid, y_pred_linear))
print("平均平方误差:", mean_squared_error(y_valid, y_pred_linear))
print("中位绝对值误差:", median_absolute_error(y_valid, y_pred_linear))
print("R2得分:", r2_score(y_valid, y_pred_linear))
​
平均绝对值误差: 0.3850644404611037
平均平方误差: 0.29041305234328235
中位绝对值误差: 0.2949103968714386
R2得分: 0.8033327254044331

验证集的评估效果看：

• 平均绝对误差0.39左右，该股票平均收盘价在14.01左右，平均误差在2.8%，对于有10%上线限制的A股来说，这个误差说明预测的效果很一般；

• 从R2看，模型对该股票未来一周内最高收盘价的解释只占到80%左右，其实这个也可以理解，毕竟影响股票价格波动的因素很多，而我们模型里只考虑了历史收盘价。

在不增加维度的情况下，模型还有没有改进或探索的余地？

我们构建的model假设未来的最高股价（因变量）只和历史收盘价（自变量）的一次方相关，显然大家会觉得不是很合理，那我们增加一下多次方看看效果，代码如下：

## 增加多项式
from sklearn.preprocessing import PolynomialFeatures
# 增加二次方项，包括交叉项，屏蔽偏置项
ploy = PolynomialFeatures(degree=2,include_bias=False)
_X_train = ploy.fit_transform(X_train)
_X_valid = ploy.fit_transform(X_valid)
_X_test = ploy.fit_transform(X_test)
​
# 模型拟合
from sklearn.linear_model import LinearRegression
_lin_reg = LinearRegression()
_lin_reg.fit(_X_train, y_train) #线性函数
​
​
from sklearn.metrics import mean_absolute_error,mean_squared_error,median_absolute_error,r2_score
y_valid_pred = lin_reg.predict(X_valid) #预测
y_train_pred = lin_reg.predict(X_train) #预测
_y_valid_pred = _lin_reg.predict(_X_valid) #预测
_y_train_pred = _lin_reg.predict(_X_train) #预测
​
print("==========================一次式模型表现=============================")
print("训练集平均绝对值误差:", mean_absolute_error(y_train, y_train_pred))
print("训练集R2得分:", r2_score(y_train, y_train_pred))
print("验证集平均绝对值误差:", mean_absolute_error(y_valid, y_valid_pred))
print("验证集R2得分:", r2_score(y_valid, y_valid_pred))
​
print("==========================多项式模型表现=============================")
print("训练集平均绝对值误差:", mean_absolute_error(y_train, _y_train_pred))
print("训练集R2得分:", r2_score(y_train, _y_train_pred))
print("验证集平均绝对值误差:", mean_absolute_error(y_valid, _y_valid_pred))
print("验证集R2得分:", r2_score(y_valid, _y_valid_pred))

==========================一次式模型表现=============================
训练集平均绝对值误差: 0.26854654331186506
训练集R2得分: 0.9727196515793944
验证集平均绝对值误差: 0.3850644404611037
验证集R2得分: 0.8033327254044331
==========================多项式模型表现=============================
训练集平均绝对值误差: 0.2483013300459851
训练集R2得分: 0.9769588366131419
验证集平均绝对值误差: 0.4274207618640246
验证集R2得分: 0.7595860527203349

        从两个模型的结果看，增加多项式后模型在训练集的表现上有了微小提升，但在验证集上性能反而下降，这个就是建模过程中会经常遇到的“模型过拟”的现象。

过拟：模型过于复杂，过渡的拟合了训练集数据，但泛化能力不足，在未知数据集上表现较差，一般通过增加模型的惩罚项（正则项）或者特征帅选来解决过拟的问题

        对线性回归模型来说，自变量前面的参数表示自身的变化对应变量带来的影响大小，我们就根据参数的大小从多西式里选出参数最大的前15个特征，为什么选15，纯粹是为了和一次项特征个数保持一致，当然大家可以实验其他的个数，具体代码和结果如下，最终在验证集上平均均对误差和R2指标上都有了一定提升。

name = ploy.get_feature_names(X_train.columns)
coef = _lin_reg.coef_
point_coef = [*zip(name,coef)]
sort_coef = pd.DataFrame(point_coef,columns=['feature','coef']).sort_values(by="coef",ascending=False)
_X_train = pd.DataFrame(_X_train,columns=name)
_X_valid = pd.DataFrame(_X_valid,columns=name)
cols = sort_coef.iloc[:15]['feature'].values
_X_train_1 = _X_train[cols]
_X_valid_1 = _X_valid[cols]
​
_lin_reg_1 = LinearRegression()
_lin_reg_1.fit(_X_train_1,y_train)
_y_valid_pred1 = _lin_reg_1.predict(_X_valid_1) #预测
_y_train_pred1 = _lin_reg_1.predict(_X_train_1) #预测
​
print("==========================多项式模型特征帅选后的表现=============================")
print("训练集平均绝对值误差:", mean_absolute_error(y_train, _y_train_pred1))
print("训练集R2得分:", r2_score(y_train, _y_train_pred1))
print("验证集平均绝对值误差:", mean_absolute_error(y_valid, _y_valid_pred1))
print("验证集R2得分:", r2_score(y_valid, _y_valid_pred1))
​
==========================多项式模型特征帅选后的表现=============================
训练集平均绝对值误差: 0.2671756549581831
训练集R2得分: 0.9730120488504624
验证集平均绝对值误差: 0.3659552057278337
验证集R2得分: 0.8144470086489938

        从筛选出的最重要的前15个特征看，大部分都是交叉影响的特征，而一次式的只有昨日收盘价，说明当日收盘价对后面几天的收盘价影响很大，符合一般散户投资心理。

['close-t-6 close-t-5', 'close-t', 'close-t-12 close-t-10',
    'close-t-11 close-t-1', 'close-t-6 close-t-1',
    'close-t-13 close-t-9', 'close-t-12 close-t-8',
    'close-t-13 close-t-11', 'close-t-7 close-t-6',
    'close-t-11 close-t-9', 'close-t-12 close-t-5',
    'close-t-11 close-t-7', 'close-t-11 close-t-4',
    'close-t-12 close-t', 'close-t-1^2']

二、模型和backtrader

        上期线性回归模型的探索就先到这了，下面我们讲下如何将模型应用到backtrader框架中去，整体的应用流程如下，其实非常简单，backtrader的基本使用如果有不清楚的可以翻一下前面的文章，或者加微信公众号交流，模型主要会在策略开发环节使用。

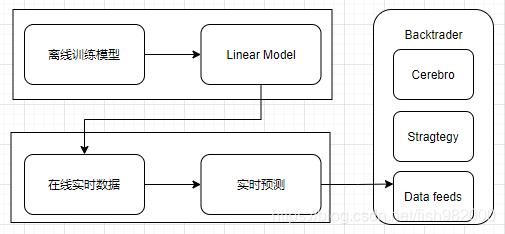
在认识backtrader一文，我们开发了一个简单策略：

买入信号：sma5上穿sma10，当时我们获取的是5分钟级别的K线数据；

卖出信号,满足下面任意一个条件：

1） sma5下穿sma10 ；

2）当前收盘价格>1.01 * 买入价格 并且 当前（sma5-sma10）< 上期(sma5-sma10) * 0.95；

3）当前收盘价格 < 0.97 * 买入价格;

现在使用模型的预测结果来发出买入或卖出信号，策略如下：

买入信号：未来5天最高收盘价格>当日收盘价格*1.01

卖出信号，满足下面任意一个条件：

1）当前收盘价格<0.95买入价格 或者 当前收盘价格>1.05买入价格；

2）持有时间最多不超过5天，在第6天按开盘价卖出

策略的代码如下：

class LinerStg(bt.Strategy):
    # 通用日志打印函数，可以打印下单、交易记录，非必须，可选
    def log(self, txt, dt=None):
        dt = dt or self.datas[0].datetime.date(0)
        print('%s, %s' % (dt.isoformat(), txt))
​
    def notify_order(self, order):
        if order.status in [order.Submitted, order.Accepted]:
            return
        if order.status in [order.Completed]:
            if order.isbuy():
                self.log('BUY EXECUTED, Price: %.6f, Cost: %.6f, Comm %.6f' %
                         (order.executed.price,
                          order.executed.value,
                          order.executed.comm))
                self.buyPrice = order.executed.price # 记录成本价
            else:
                self.log('SELL EXECUTED, Price: %.6f, Cost: %.6f, Comm %.6f' %
                         (order.executed.price,
                          order.executed.value,
                          order.executed.comm))
        return super().notify_order(order)
​
    def __init__(self):
        self.dataClose = self.datas[0].close
        self.maxClose = self.datas[0].pred
        self.buyPrice = None
        self.holdDays = 0
       
​
    def next(self):
        if self.holdDays > 0:
            self.holdDays = self.holdDays + 1;
            
        if not self.position:  # not in the market
            if self.maxClose[0] > self.dataClose[0] * 1.01:  # 预测未来最高收盘价涨幅超过%5，买入
                self.buy()  # enter long
                self.holdDays = 1
​
        else:
            if self.dataClose[0] < self.buyPrice * 0.95 or self.dataClose[0] > self.buyPrice * 1.05:  # 止盈或止损
                self.close()  # close long position
            elif self.holdDays>6: # 持有5天后，如果还是没有触发卖出信号，则第6天卖出
                self.close()

最终该策略在测试数据集上的回测表现结果如下，表现结果还不错，但这不能说明我们的策略很ok，从趋势看该股票在测试期间表现很强势，在这种情况下基本所有的策略表现都不会差，一个好的成熟的策略需要禁得起不同市场的检验。

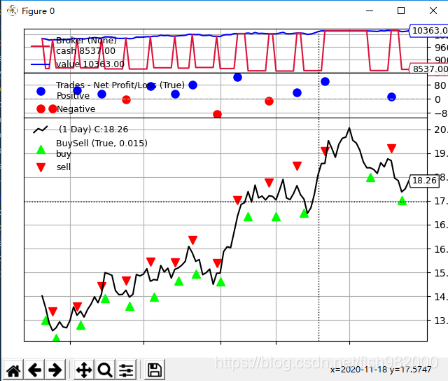
我们看下入门篇里简单的快慢均线策略在该数据集上的回测表现，结果也还不错，所以有时候我们在股票市场赚钱不是我们厉害，只是市场实在太好，想亏钱都难。

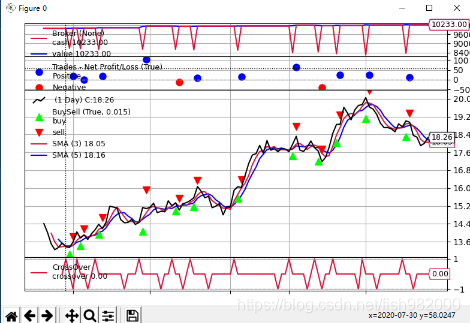
总结：

        今天主要回顾了一下之前开发的线性模型，并做了初步探索和完善，理论上说线性模型是凸函数，凸函数肯定是可以找到全局最优的，我们调用的sklearn库也正是直接解线性函数得到的全局最优解，后面打算自己手写一个线性模型，用机器学习领域更常见的梯度下降来求最优解，并和sklearn做对比，从而来讲讲梯度下降求最优值时需要注意的一些事情。

        还是一句话：有什么问题，欢迎加微信公众号，线上交流~